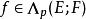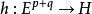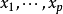交錯多重線性映射

交錯多重線性映射(alternating multilinear mapping)是一種特殊的反對稱多重線性映射。其定義是：設映射f∈￡_p(E;F)，如果只要至少對於一個指標i（1≤i<p），x_i=x_i+1，f(x₁,…,x_p)就是零，那么映射f就叫做交錯的。（約定，對於p=1，任何線性映射E→F是交錯的。）

基本介紹

• 中文名：交錯多重線性映射
• 外文名：alternating multilinear mapping
• 性質：一種特殊的反對稱多重線性映射
• 相關：多重線性映射
• 一級學科：數學
• 二級學科：多重線性代數

簡介

交錯多重線性映射(alternating multilinear mapping)是一種特殊的反對稱多重線性映射。設

為多重線性映射（其中V，W都是域K上的線性空間），若對任意的 ，當 時，必有 ，則稱 為交錯多重線性映射。由於偶(奇)置換必可分解為偶(奇)數個對換之積，利用 的多重線性性質展開 ，即知交錯多重線性映射一定是反對稱多重線性映射，反過來未必成立，但在K的特徵不為2(特別是K的特徵為0，例如K=C時)二者是等價的概念。

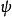
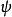
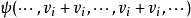
性質

E及F重新表示兩個賦范巴拿赫空間。

命題：設f∈￡_p(E;F)是一個交錯多重線性映射，那么：

（1）每當對於一對不同的指標（i，j），我們有x_i=x_j時，就有f(x₁,…,x_p)=0；

（2）對於序列[1,…,p]的任何排列σ，我們有

其中ε(σ)=±1是排列σ的標記。

反對稱多重線性映射

一類重要的多重線性映射。關於G和χ對稱的多重線性映射

當G=S_m，χ=ε（稱號特徵標，σ∈S_m為偶（奇）置換時ε(σ)=1(-1)）時，稱為反對稱多重線性映射，簡稱反對稱映射。或等價地定義為：當對任意σ∈S_m有

時，稱為反對稱多重線性映射。當域K的特徵為0時，多重線性映射

為反對稱的若且唯若對任意的（i≠j），當時，有。在域K之特徵非0時，這二者未必等價。

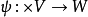
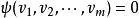
交錯多重線性映射的乘法

設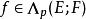並且為了定義 f 及 g 之間的乘積，必須先給出一個連續雙線性映射

（在一個賦范e.v.H中取值）。於是連帶著 f 及 g，可取一映射，即

映射 h 顯然是連續多重線性的。但它一般不是交錯的：它只屬於（p+q）重線性映射的向量空間；這種映射作為前p個變數的映射是交錯的，作為後q個變數的映射也是交錯的，把這種空間記作。