基本介紹
- 中文名:線性變換
- 外文名:linear mapping
- 屬於:數學名詞
- 定義:線性空間V到W的保線性的映射
- 套用學科:數學
- 別名:線性映射
定義
 線性變換參考圖
線性變換參考圖性質
運算


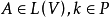
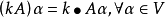



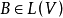
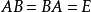
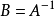
理解
 線性變換參考圖
線性變換參考圖 雙線性變換圖
雙線性變換圖 線性變換算式
線性變換算式 線性變換算式
線性變換算式 線性變換參考圖
線性變換參考圖
線性映射一般指本詞條
 線性變換參考圖
線性變換參考圖

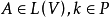
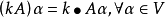



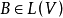
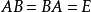
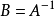
 線性變換參考圖
線性變換參考圖 雙線性變換圖
雙線性變換圖 線性變換算式
線性變換算式 線性變換算式
線性變換算式 線性變換參考圖
線性變換參考圖線性映射矩陣(matrix of a linear mapping)是一種特殊矩陣,指線性映射的數量表示。設σ是數域P上n維線性空間V到P上m維線性空間W的一個線性映射,v1,v2,…,vn...
線性映射( linear mapping)是從一個向量空間V到另一個向量空間W的映射且保持加法運算和數量乘法運算,而線性變換(linear transformation)是線性空間V到其自身的線性...
幾乎開線性映射是一類重要的線性映射,幾乎開映射可用來刻畫桶型空間。...... 幾乎開線性映射是一類重要的線性映射,幾乎開映射可用來刻畫桶型空間。中文名 幾乎開線性...
雙曲線性映射亦稱雙曲線性同構,是沿一個方向擴張,沿另一個方向收縮的可逆線性映射。線性映射的雙曲性經過小擾動之後不至於被破壞,這一性質在動力系統結構穩定性的...
半線性映射(semi-linear mapping)是線性映射概念的推廣。線性映射亦稱同態或線性同態。線性代數的中心內容和基本概念之一。線性空間亦稱向量空間。它是線性代數的中心...
在數學裡,線性函式是指那些線性的函式,但也常用作一次函式的別稱,儘管一次函式不一定是線性的。線型函式是一個比較恰當的同義詞。...
伴隨映射(adjoint mapping)是一種映射。內積空間中的共扼映射。設E,F是域K上的內積空間,φ:E→F,φ':F→E是線性映射。若∀ x∈E,y∈F,(φx,y)=(x...
交錯多重線性映射(alternating multilinear mapping)是一種特殊的反對稱多重線性映射。其定義是:設映射f∈£p(E;F),如果只要至少對於一個指標i(1≤i
線性代數的重要概念之一.設σ是數域P上的線性空間V的一個變換.若對於V中的任意向量α,β與P中的任意數k,有σ(α+β)=σ(α)+σ(β),σ(kα)=kσ(...
復化線性映射(complexified linear map)是復向量空間間的線性映射被復化。...... 復化線性映射(complexified linear map)是復向量空間間的線性映射被復化。...
線性同胚(linear homeomorphism)是用來刻畫兩個拓撲線性空間結構相似性的概念。...... 稱Φ是E和F之間的一個線性同胚映射,而此時稱E和F是線性同胚的,或是線性拓撲...
帳篷映射(tent map),在數學中是指一種分段的線性映射,因其函式圖像類似帳篷而得名。...
介紹 結構映射(structural mapping)一類特殊的映射.刻畫代數中乘法或賦予向量空間一個乘法的映射.若A是一個代數,乘法AXA->A確定一個線性映射}}:AOX.9->A,使f}...
在數學裡,映射是個術語,指兩個元素的集之間元素相互“對應”的關係,為名詞。映射,或者射影,在數學及相關的領域經常等同於函式。 基於此,部分映射就相當於部分...
張映射((spread mapping)多重線性代數的重要概念.具有因子化泛性質的多重線性映射...... ((spread mapping)多重線性代數的重要概念.具有因子化泛性質的多重線性映...
整線性變換是線性變換的一種。設k≠0,h為常數,稱w=kz+h為整線性變換。特別地,當h≠0時,稱映射w=z+h為平移映射。...
線性相關同態映射(linearly dependent ho-momorphic mappings)伽羅瓦理論的重要概念.設K,K'是F的兩個擴域,是當K,K‘作為F代數時,從K到K‘的代數同態(這樣的...
s映射(S-map)一種簡單的一維非線性映射.其具體形式為 它由間隔[o,l」到其自身的映射中,僅在二胡處有一個最大值,並且f.(二)處處有負的施瓦茲導數,即 顯然...
可逆線性變換(invertible linear transformation)亦稱非退化線性變換,或滿秩線性變換,是一種特殊的線性變換,設V是數域P上的線性空間,σ是V的線性變換,若存在V的...
整線性變換w=kz+h包括平移映射和伸縮與旋轉映射。特別地,當h≠0時,稱映射w=z+h為平移映射。平移映射w=z+h可看成將向量z沿向量h的方向平行移動一段距離|h...
向量空間又稱線性空間,是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後,使許多問題的處理變得更為簡潔和清晰,在此基礎上的進一步抽象化,形成了與...
