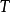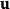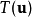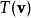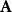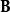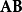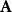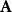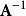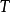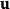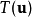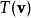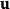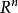在線性代數中,正交變換是線性變換的一種,它從實內積空間V映射到V自身,且保證變換前後內積不變。
因為向量的模長與夾角都是用內積定義的,所以正交變換前後一對向量各自的模長和它們的夾角都不變。特別地,標準正交基經正交變換後仍為標準正交基。
在有限維空間中,正交變換在標準正交基下的矩陣表示為正交矩陣,其所有行和所有列也都各自構成V的一組標準正交基。因為正交矩陣的行列式只可能為+1或−1,故正交變換的行列式為+1或−1。行列式為+1和−1的正交變換分別稱為第一類的(對應旋轉變換)和第二類的(對應瑕旋轉變換)[2]。可見,歐幾里得空間中的正交變換隻包含旋轉、反射及它們的組合(即瑕旋轉)。
正交變換的逆變換也是正交變換,後者的矩陣表示是前者矩陣表示的逆。
基本介紹
- 中文名:正交變換
- 外文名:orthogonal mapping
- 學科:數學
- 屬於:線性變換
- 包含:旋轉和軸對稱
- 性質:逆變換也是正交變換
定義
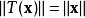
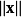
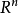
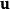

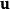

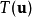
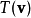

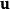
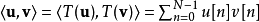
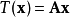
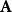
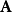
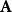
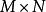
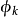
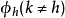
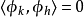
等價刻畫
正交矩陣
分類
性質