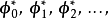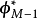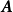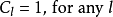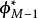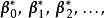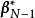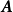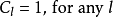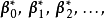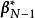離散正交轉換

數學上，任一的MxN離散線性轉換皆可表示成矩陣（Matrix） 的型式：Y=AX，再進一步假設，若矩陣Aby正交基底 (Orthogonal basis) 列向量（Row vector） 所組成，也可表示成級數和形式。

基本介紹

• 中文名：離散正交轉換
• 外文名：Discrete orthogonal transform
• 分類：數理kex

離散正交轉換

大致上，可簡單化將矩陣分類由（a）列向量（Row Vector）或（b）行向量（Column Vector）所組成。

正交矩陣by列向量：

若

其中， 和 為一組列向量的正交集合且稱 為一種離散正交轉換。

再者，若滿足 。則 和 將組成一組列向量的正規化正交集合且稱 為一種離散正規化正交轉換。

此時，我們可利用 和 來求得 的反矩陣：

其中 。再者，也可表示成級數和（Summation）形式：

若 ，即簡化成，

正交矩陣by行向量：

若

其中， 和 為一組行向量的正交集合且也稱 是一種離散正交轉換。

再者，若滿足 。則 和 將組成一組行向量的正規化正交集合且稱為一種離散正規化正交轉換。

此時，我們再利用 和 來組成 的反矩陣：

其中 。再者，也可表示成級數和：

若 ，即簡化成，

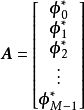
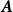
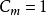
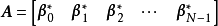
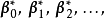
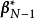
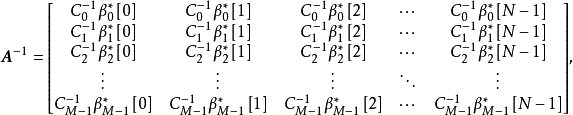
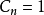
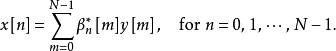
例子

• 離散傅立葉變換
  
• 離散餘弦變換、離散正弦變換、離散哈特利轉換
  
• 瓦希轉換、哈爾小波轉換
  
• 離散勒詹德轉換
  
• 離散正交多項式轉換
  

如：哈恩轉換、Krawtchouk多項式、Charlier多項式。

特性

• 其列向量型式與行向量型式為一體兩面的情形：
  

順向轉換（Forward Transform）：列向量型式 反向轉換（Inverse Transform）：行向量型式。

順向轉換（FT）：行向量型式 反向轉換（IT）：列向量型式。

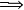
• 於正規化正交情況下：
  

若為行向量所組成的正規化正交矩陣，則它所對應的列向量形成的反矩陣 必為正規化正交矩陣。

若為列向量所組成的正規化正交矩陣，則它所對應的行向量形成的反矩陣 必為正規化正交矩陣。

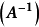
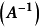
優點

• 彼此間的列向量（或行向量）不會互相產生干擾（Interference）。
  在同一維度（dimension）下，DOT提供正交矩陣內的列向量（或行向量） 彼此間重要的正交特性，可藉由此避免其他使用者干擾進而來實現多工存取技術。
  

其本身的FT與對應的IT結構為相當類似。

• 此外，離散正交轉換較非正交轉換（Non-orthogonal Transform）計算上較為簡單。
  
• 將DOT套用於影像重建（Reconstruction） 或壓縮上，可藉由增加正交基底（Orthogonal basis）來控制誤差的產生，是採用非正交轉換所能及的。