基本介紹
- 中文名:快速小波變換
- 外文名:Fast wavelet transform
定義
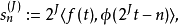
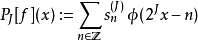
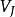
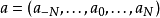
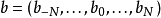
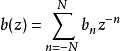
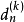
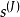
前項離散小波轉換
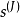
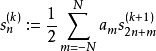
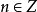
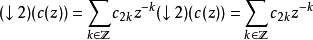
加星標的Laurent多項式
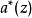
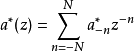
乘法是多項式乘法,相當於係數序列的卷積。
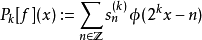
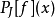
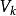
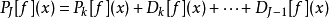
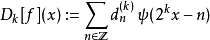
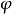
離散小波變換
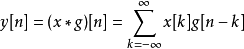
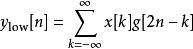
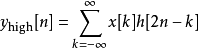
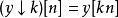
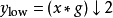
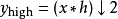
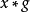
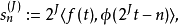
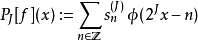
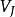
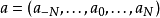
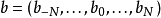
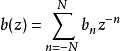
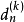
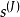
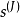
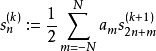
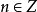
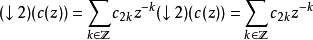
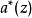
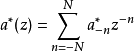
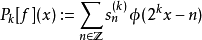
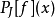
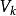
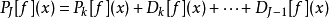
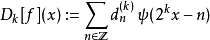
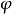
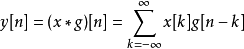
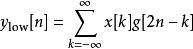
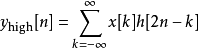
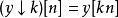
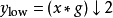
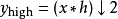
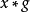
快速小波變換,也叫快速小波轉換(英語:Fast wavelet transform)是利用數學的演算法則用來轉換在時域的波形或信號變成一系列的以正交基底構成的小而有限的波、小波。 ...
快速小波轉換(英語:Fast wavelet transform)是利用數學的演算法則用來轉換在時域的波形或信號變成一系列的以正交基底構成的小而有限的波、小波。 當然,快速小波轉換...
小波變換(wavelet transform,WT)是一種新的變換分析方法,它繼承和發展了短時傅立葉變換局部化的思想,同時又克服了視窗大小不隨頻率變化等缺點,能夠提供一個隨頻率...
該式定義了連續小波變換,a為尺度因子,表示與頻率相關的伸縮,b為時間平移因子。...同時,作為視窗函式,為了保證時間視窗與頻率視窗具有快速衰減特性,經常要求函式ψ(...
本書重點介紹小波技術及其在信號、圖像與圖形處理中的套用,涵蓋了經典小波、細分小波與雙樹復小波。基礎部分內容包括多分辨分析的概念、一維二維離散小波變換及其Mallat...
相對於Mallat塔形算法而言,第二代小波方法是一種更為快速有效的小波變換實現方法,它的優勢有以下四點:(1)它不依賴於Fourier變換,完全在時域中完成對雙正交小波的...
二進小波變換(dyadic wavelet transform)由二進制小波決定的變換.設}(x)是二進小波,令 為二進小波變換.二進小波變換是連續小波變換半離散化的結果.人們只是把...
詳細分析了小波變換的基本原理,詳細闡述了多分辨逼近和小波分解的基本思想,詳細討論了離散小波變換及其快速算法的實現過程,介紹了幾種常用的小波及其構造方法,還給出...
小波函式:又稱凌波函式、小波分析(wavelet analysis), 或小波變換、小波轉換(wavelet transform)是指用有限長或快速衰減的、為母小波(mother wavelet)的震盪波形來...
《小波變換與圖像處理》是作者在十多年的小波教學和科研實踐的基礎上,總結、整理教學講義和科研成果而成的。...
離散二進小波變換(discrete dyadic wavelet transform)是離散信號的二進小波變換。...... 離散二進小波變換(discrete dyadic wavelet transform)是離散信號的二進小波...
小波分析是當前套用數學和工程學科中一個迅速發展的新領域,經過近30年的探索研究,重要的數學形式化體系已經建立,理論基礎更加紮實。與Fourier變換相比,小波變換是空間...
小波變換(Wavelet Transfom)編碼是數字地球的最有發展前途的數據壓縮方法。小波分析優於傅立葉分析的方面是:它的時間域或頻率域同時具有良好的局部化性質,而且由於...
小波變換與圖像壓縮系統的學位授予單位是中山大學...... 本詞條缺少名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!小波變換與圖像壓縮系統的學位授予單...
小波變換是一種用於決定卷積的特定視窗函式,提供了將圖像分解成不同尺度組成的一種數學框架。成百種不同的小波函式被提出用來增強或模糊特定的特徵。二維的離散傅里...
書中清楚地給出了傅立葉、小波和時頻變換的標準表示,以及用快速算法構造的正交基。作者在解釋了稀疏的主要概念後將其運用於信號壓縮、噪聲衰減和逆問題,同時給出...
二進小波變換重構公式(resolution of the iden-tity for dyadic wavelet transform)二進小波變換的基本性質.關於一個二進小波}(x)的二進小波變換重構公式為 ...
小波分析是目前數學中一個迅速發展的新領網域,它同時具有理論深刻和套用十分廣泛的雙重意義。小波變換的概念是由法國從事石油信號處理的工程師J.Morlet在1974年首先...
2.3.2墨西哥帽小波17 2.3.3Haar小波18 2.4連續小波變換算法19 2.5離散小波變換21 2.5.1多解析度分析21 2.5.2快速金字塔算法23 2.5.3二維抽取小波變換25 2.6...
對一個給定信號進行小波變換,就是將該信號按某一小波函式簇展開。...... 補充相關內容使詞條更完整,還能快速升級,趕緊...對一個給定信號進行小波變換,就是將該信號...
本詞條缺少名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!二進小波...二進小波變換是由二進小波決定的變換。設ψ(x)是二進小波,令 這時f(x)在...
6.7.3 利用梅林變換(Mellin Transform)進行快速計算 第7章 離散小波變換 7.1 尺度和位移的離散化方法 7.2 時頻離散化重構原信號——框架 7.3 標架概...
