漢克爾變換是指對任何給定函式 以第一類貝塞爾函式作無窮級數展開,貝塞爾函式 的階數不變,級數各項作變化。
基本介紹
- 中文名:Hankel變換
- 外文名:Hankel transform
- 分類:數理科學
定義,正交性,與其他函式變換的關係,傅立葉變換,
定義
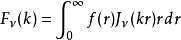
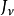
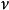
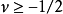
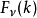
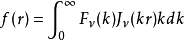
正交性
貝塞爾函式構成正交函式族權重因子為r:
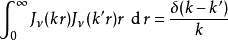
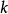
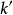
與其他函式變換的關係
傅立葉變換
零階漢克爾函式即為圓對稱函式的二維傅立葉變換。給定二維函式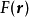 ,徑向矢量為
,徑向矢量為 ,其傅立葉變換為
,其傅立葉變換為
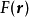

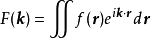
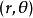
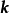
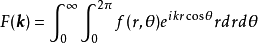
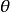
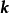

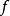
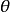
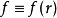
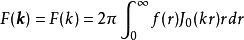
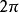
漢克爾變換是指對任何給定函式 以第一類貝塞爾函式作無窮級數展開,貝塞爾函式 的階數不變,級數各項作變化。
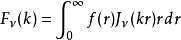
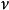
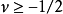
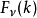
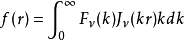
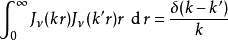
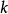
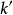
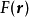

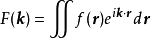
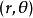
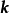
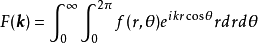
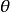
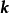

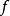
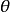
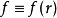
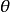
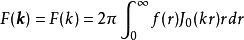
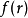
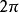
漢克爾變換是指對任何給定函式 以第一類貝塞爾函式作無窮級數展開,貝塞爾函式 的階數不變,級數各項作變化 [1] 。中文名 Hankel變換 外文名 Hankel transform ...
5.3 用Mellin變換解積分方程1265.4 Hankel變換 有限Hankel變換130參考文獻132習題132第6章 第一類Fredholm方程1376.1 特徵值與特徵函式 退化核方程137...
5.7 分數傅立葉變換 5.8 Hankel變換 5.9 Radon變換 5.10 幾何變換 5.11 Hough變換 參考文獻 習題 第6章 光學互連 6.1 引言 6.2 聚合物波導 6.3 薄膜波導...
一、WD變換 二、小波變換 三、小波變換套用 四、二維CWT 第五章 圖像變換與增強 第一節 二維變換 一、二維傅氏變換和Hankel變換 二、Hankel變換 第二節 其他圖...
5.3.2Hankel變換及求解5.4z變換及其反變換5.4.1z變換及反變換定義與性質5.4.2z變換的計算機求解5.5複變函數問題的計算機求解5.5.1複數矩陣及其變換...
6.2.4 Laplace變換域中二維固結問題的基本解6.3 橫向無限區域非飽和多孔介質的軸對稱固結問題6.3.1 Laplace變換域固結方程的Hankel變換解...
