定義
與傅立葉變換不同的是,在變換式中用正、餘弦函式之和,即cast=cost+sint來取代傅立葉變換式中的復指數函式e=cost+jsint,所以當信號x(t)是實函式(波形為實數值)時,變換式只有實數運算,即
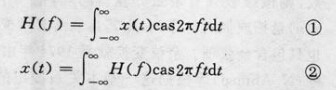 圖1 公式
圖1 公式式①、②定義為哈特萊變換對,其中H(f)稱為x(t)的正變換,x(t)稱為H(f)的逆變換。與傅立葉變換相比,其特點為:①變換式H(f)是實數,它不同於傅立葉變換F(f)是複數;②正變換和逆變換的運算完全一樣,是一對實的嚴格互逆的積分變換,因此很適於作實數據的譜分析和卷積運算。
為了便於計算機計算,對式①、②分別在時域和頻域進行離散化,可得長度為N,實序列x(n)的一對離散哈特萊變換(DHT),其定義式為圖2。
 圖2 公式
圖2 公式式中k,n分別代表頻率離散變數和時間離散變數。N=2,r為正整數。哈特萊變換是實波形描述的一種形式,它與實信號的傅立葉變換有著密切的內在聯繫。可以證明x(n)的離散傅立葉變換F(k),等於x(n)的離散哈特萊變換H(k)的偶部He(k)減虛數j乘以奇部H0(k),F(k)=He(k)-jH0(k)。按H(k)=He(k)+H0(k),所以通過DHT可以避免複雜的複數運算,方便地求得DFT。特別對功率譜和相位譜的求解,還存在下列簡單關係。
功率譜圖3,相位譜圖4
 圖3 公式
圖3 公式 圖4 公式
圖4 公式DHT也有快速哈特萊蘇昂奮(FHT),可套用於快速傅立葉變換(FFT)所能套用的領域。FHT與實數據FFT或最佳的FFT算法的運算速度基本上一樣,在某些套用場合略快些。後來人們不斷地對DHT進行研究,提出了各種一維和二維的快速算法。其中採用二維DHT計算二維DFT,由於主要是實數計算,所以具有運算量少,便於算法實現等優點,因而在圖像處理、模式識別等領域獲得套用。
性質
哈特萊變換具有傅氏變換的大部分特徵,其性質也與傅氏變換相似B r a c e w e l l,s a a t c i la 等人對此作了一些討論。在此通過與傅氏變換的類比,歸納、總結、補充了哈特萊變換的各種性質如下:
對稱定理
若f(t)的哈特萊變換為H(f),那么H(t)的哈特萊變換為f(f)。這從哈特萊變換的定義即可得到證明。可見哈特萊變換比傅氏變換更加對稱。
時移定理
設f(t)的哈特萊變換為H(f),那么f(t-to)的哈特萊變換為圖5
 圖5 公式
圖5 公式式中:H為哈特萊變換運算元。
頻移定理
假定H(f)是f(t)的哈特萊變換,那么哈特萊變換分別為圖6
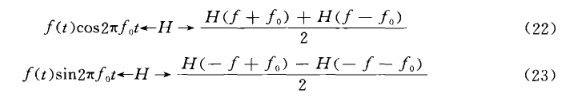 圖6 公式
圖6 公式時域微分定理
時域微分定理
設f(t)的哈特萊變換為H(f),那么有圖7
 圖7 公式
圖7 公式這是一個非常有用的性質,它涉及函式導數的哈特萊變換,在解決有關波動方程的問題時常會用到這個性質。儘管它比較複雜,但仍可以用統一的公式來表達。利用傅氏變換與哈特萊變換的關係可以證明該定理。
奇偶性
哈特萊變換不改變函式的奇偶性。在正變換中,H(f)的奇偶性與f(t)一致;在反變換中,f(t)的奇偶性與H(f)一致。
褶積定理
若f1(t)與f2 (t)的哈特萊變換分別為H1(f)和H2(f),那么由式(16)和奇偶性可得圖8
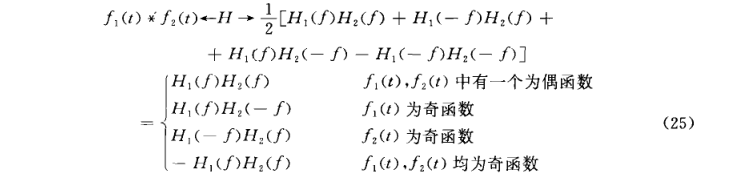 圖8 公式
圖8 公式乘積定理
若f1(t)與和f2(t)的哈特萊變換分別為H1(f)和H2(f),那么如圖9
 圖9 公式
圖9 公式相關定理
(l)自相關
若 f ( t)的哈特萊變換為 H ( f ),那么的哈特萊變換為圖10:
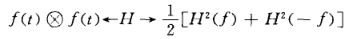 圖10 公式
圖10 公式(2)互相關
若 f 1( t)的哈特萊變換為 H1 ( f ), 那么 f2( t)的哈特萊變換為 H2( f )那么的哈特萊變換為圖11:
 圖11 公式
圖11 公式傅氏變換在機率論中有廣泛的用途,它常作為密度函式和自相關函式的傅氏變換以及穩定隨機過程的譜分布而出現的。而矩在機率論中是一個非常重要的概念。下面我們給出哈特萊變換中的矩定理。
設f(t)的哈特萊變換為H(f),定義函式f(t)的n階矩為圖12
 圖12 公式
圖12 公式則矩定理可表示為圖13
 圖13 公式
圖13 公式 圖1 公式
圖1 公式 圖2 公式
圖2 公式 圖3 公式
圖3 公式 圖4 公式
圖4 公式 圖5 公式
圖5 公式 圖6 公式
圖6 公式 圖7 公式
圖7 公式 圖8 公式
圖8 公式 圖9 公式
圖9 公式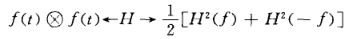 圖10 公式
圖10 公式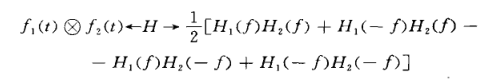 圖11 公式
圖11 公式 圖12 公式
圖12 公式 圖13 公式
圖13 公式