基本介紹
- 中文名:列向量
- 外文名:column vector
- 學科:數理科學
- 類型:數學術語
- 定義:一個 n×1 的矩陣
- 轉置:行向量
向量
簡介




單位列向量

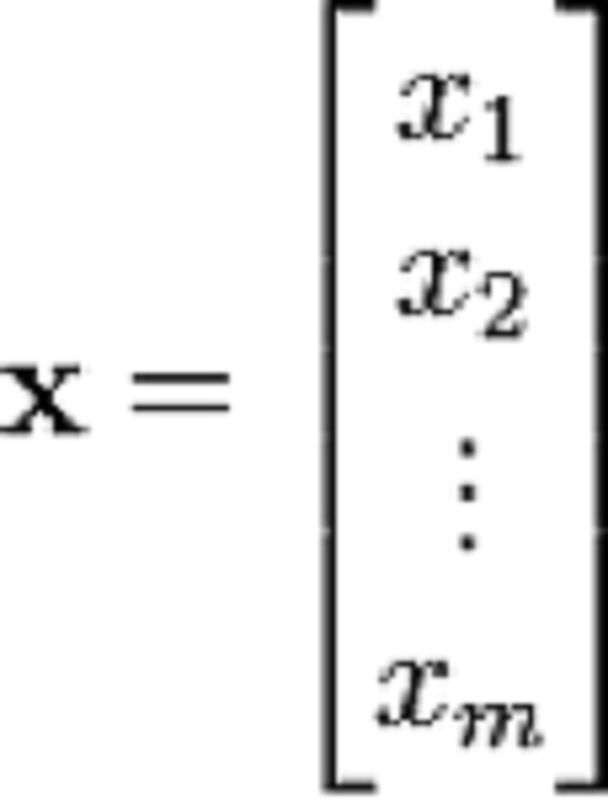





線上性代數中,列向量是一個 n×1 的矩陣,即矩陣由一個含有n個元素的列所組成:列向量的轉置是一個行向量,反之亦然。所有的列向量的集合形成一個向量空間,它...
線上性代數中,行向量是一個 1×n的矩陣,即矩陣由一個含有n個元素的行所組成即行向量。行向量的轉置是一個列向量,反之亦然。所有的行向量的集合形成一個向量...
定義 最終產品列向貴(column vector of final products)投人產出分析術語.指一定時期經濟系統內各部門向全社會提供的最終產品數量組成的列向量.最終產品y, (2一1...
列矩陣又稱列向量,是指有一列的矩陣。如果矩陣 A=(aij)m×n只有一行,即m=1,則此時稱之為行矩陣,或行向量。同樣,若 A=(aij)m×n只有一列,即n=1,這時...
n階複方陣U的n個列向量是U空間的一個標準正交基,則U是酉矩陣(Unitary Matrix)。顯然酉矩陣是正交矩陣往複數域上的推廣。酉矩陣又稱為么正矩陣。在2000年之前...
線上性代數中,一個矩陣A的列秩是A的線性獨立的縱列的極大數目。類似地,行秩是A的線性獨立的橫行的極大數目。矩陣的列秩和行秩總是相等的,因此它們可以簡單地...
線上性代數中,行向量或行矩陣是1×m階矩陣,即由單行m個元素組成的矩陣,記作A=(a1 a2…am),為避免元素間的混淆,也記作A=(a1,a2,…an)。...
線性獨立一般是指向量的線性獨立,指一組向量中任意一個向量都不能由其它幾個向量線性表示。...
(線性復向量空間)來表述,即Hilbert 空間可以表述量子系統的各種可能的量子態.為了便於表示和運算,Dirac提出用符號 x〉 來表示量子態,x〉 是一個列向量,稱為ket ...
求出的n個變數所構成的列向量X=(x1,···xn)T,若能再滿足非負條件(即決策變數滿足所有約束條件),稱為線性規則問題的可行解。使得目標函式值z達到max最大的...
1.將矩陣的列向量依次一個向量接一個向量地組成一個長向量.如基是nXm階矩陣,記vec(遨)-(a,1 , a2,,…,a,a,a}z,azz,…,anz,…,a,二)T,稱vec為按...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
這些是M*M及MM*的奇異值,並與U和V的列向量相對應。奇異值和奇異向量, 以及他們與奇異值分解的關係一個非負實數σ是M的一個奇異值僅當存在Km 的單位向量u和...
特徵值是線性代數中的一個重要概念。在數學、物理學、化學、計算機等領域有著廣泛的套用。設 A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,...
列昂捷夫逆矩陣(Lconticf inversc matrix)投入產出模型中的一個重要數學概念。由*列昂捷夫首先提出,故稱。令X為各部門總產值列向量,I為單位矩陣,A為直接消耗係數...
