轉置是一個數學名詞。直觀來看,將A的所有元素繞著一條從第1行第1列元素出發的右下方45度的射線作鏡面反轉,即得到A的轉置。一個矩陣M, 把它的第一行變成第一列,第二行變成第二列,......,最末一行變為最末一列, 從而得到一個新的矩陣N。 這一過程稱為矩陣的轉置。即矩陣A的行和列對應互換。
基本介紹
- 中文名:轉置
- 外文名:transposition
- 性質:數學名詞
- 公式:A=(aij)m×n
- 運用:矩陣
- 學科:數理科學
定義
公式介紹

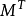



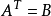

基本性質

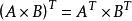


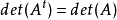
正交矩陣
套用





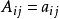



轉置是一個數學名詞。直觀來看,將A的所有元素繞著一條從第1行第1列元素出發的右下方45度的射線作鏡面反轉,即得到A的轉置。一個矩陣M, 把它的第一行變成第一列,第二行變成第二列,......,最末一行變為最末一列, 從而得到一個新的矩陣N。 這一過程稱為矩陣的轉置。即矩陣A的行和列對應互換。

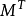



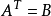


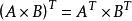


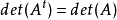





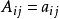


轉置是一個數學名詞。直觀來看,將A的所有元素繞著一條從第1行第1列元素出發的右下方45度的射線作鏡面反轉,即得到A的轉置。一個矩陣M, 把它的第一行變成第一...
將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。...... 將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。中文名 轉置矩陣 外...
矩陣轉置編輯 鎖定 相關概念 矩陣(Matrix)本意是子宮、控制中心的母體、孕育生命的地方。在數學上,矩陣是指縱橫排列的二維數據表格,最早來自於方程組的係數及常數所...
共軛轉置編輯 鎖定 若矩陣A、B維數相同,則(A + B)* = A* + B*。 (rA)* = r*A*,其中r為複數,r*為r的復共軛。中文名 共軛轉置 外文名 Conjugate...
流圖轉置(flow graph transposition)網路結構的一種變換方法.信號流圖中,將所有支路的方向倒置,並且將輸入與輸出對應交換,這種變換稱為流圖轉置.流圖轉置以後,其輸...
語言獲得轉置編輯 鎖定 本詞條缺少名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!心理言語學家喬姆斯基在20世紀50年代創立轉換生成語法理論(...
鐵路換算用轉置是指反映鐵路運輸業完成全部運輸工作任務情況的綜合生產指標。其計算方法是,將以噸公里為單位的貨物周轉量與以人公里為單位的旅客周轉量,以及以噸公里...
正定矩陣是一種實對稱矩陣。正定二次型f(x1,x2,…,xn)=X′AX的矩陣A(或A的轉置)稱為正定矩陣。線上性代數裡,正定矩陣 (positive definite matrix) 有時會...
TRANSPOSE,函式,可返回轉置單元格區域,即將行單元格區域轉置成列單元格區域,反之亦然。...
對稱矩陣(Symmetric Matrices)是指元素以主對角線為對稱軸對應相等的矩陣。線上性代數中,對稱矩陣是一個方形矩陣,其轉置矩陣和自身相等。1855年,埃米特(C.Hermite,...
n階複方陣A的對稱單元互為共軛,即A的共軛轉置矩陣等於它本身,則A是埃爾米特矩陣(Hermitian Matrix)。顯然埃爾米特矩陣是實對稱陣的推廣。...
矩陣運算在科學計算中非常重要 [9] ,而矩陣的基本運算包括矩陣的加法,減法,數乘,轉置,共軛和共軛轉置 [1] [10] 。矩陣加法 矩陣的加法滿足下列運算律(A,B,...
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...
線上性代數中,列向量是一個 n×1 的矩陣,即矩陣由一個含有n個元素的列所組成:列向量的轉置是一個行向量,反之亦然。所有的列向量的集合形成一個向量空間,它...
線上性代數中,行向量是一個 1×n的矩陣,即矩陣由一個含有n個元素的行所組成即行向量。行向量的轉置是一個列向量,反之亦然。所有的行向量的集合形成一個向量...
