正規矩陣在數學中是指與自己的共軛轉置矩陣對易的復係數方塊矩陣。任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣的矩陣都是正規矩陣。
基本介紹
- 中文名:正規矩陣
- 外文名:Normal matrix
- 學科:線性代數
定義,性質,
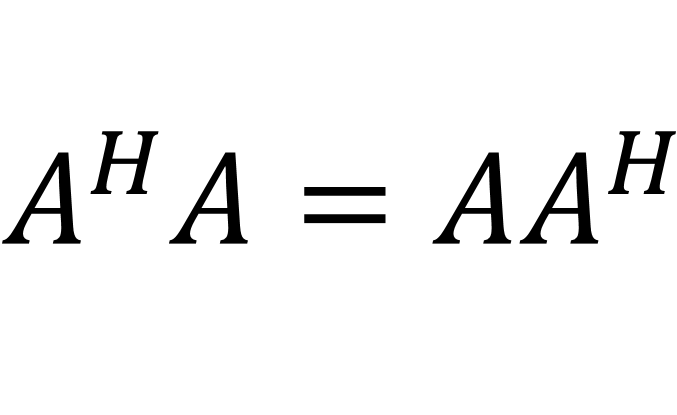
正規矩陣在數學中是指與自己的共軛轉置矩陣對易的復係數方塊矩陣。任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣的矩陣都是正規矩陣。
正規矩陣在數學中是指與自己的共軛轉置矩陣對易的復係數方塊矩陣。任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣...
一個n階方陣如果滿足,其所有元素均大於等於0,且每一行的元素之和為1,則稱方陣為機率矩陣。...
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
《矩陣分析》是2005年機械工業出版社出版的圖書,由(美)合恩(Horn.R.A.)創作,楊奇翻譯。該書是一本對數值計算研究人員來說標準的參考書。本書從數學分析的角度...
埃爾米特矩陣(又稱“自共軛矩陣”)是共軛對稱的方陣。埃爾米特矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等。n階複方陣A的對稱單元互...
《矩陣理論及方法》是2012年科學出版社出版的圖書,作者是謝冬秀、雷紀剛、陳桂芝。本書主要介紹了工程實際中有套用價值的矩陣理論與方法。...
矩陣分析是由清華大學出版社出版的一本主要關於矩陣的分解和矩陣函式的矩陣分析圖書。...
矩陣論教程是由機械工業出版社出版的書籍,作者是張紹飛 趙迪,在2012-05-31出版。本書主要講解矩陣的基本理論與方法。...
