基本介紹
- 中文名:酉矩陣
- 外文名:Unitary Matrix
- 又稱:么正矩陣
- 判別準則:酉矩陣共軛轉置和其逆矩陣相等
- 一級學科:數學
- 二級學科:矩陣
定義




判別準則

性質和套用






廣義酉矩陣
定義









性質





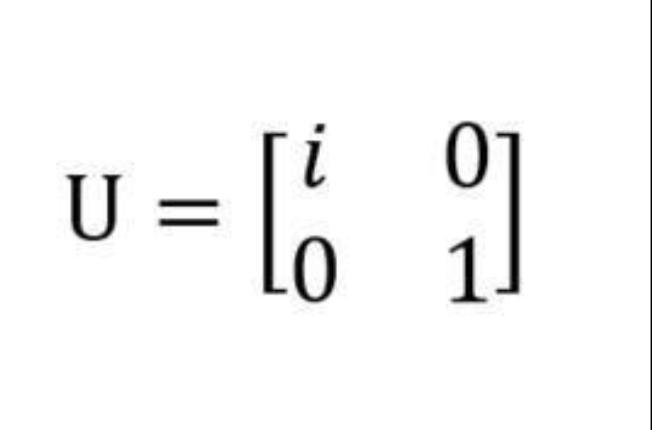

























n階複方陣U的n個列向量是U空間的一個標準正交基,則U是酉矩陣(Unitary Matrix)。顯然酉矩陣是正交矩陣往複數域上的推廣。酉矩陣又稱為么正矩陣。在2000年之前...
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。矩陣是高等...
正規矩陣在數學中是指與自己的共軛轉置矩陣對易的復係數方塊矩陣。任意正規矩陣都可在經過一個酉變換後變為對角矩陣,反過來所有可在經過一個酉變換後變為對角矩陣...
埃爾米特矩陣(又稱“自共軛矩陣”)是共軛對稱的方陣。埃爾米特矩陣中每一個第i 行第j 列的元素都與第j 行第i 列的元素的共軛相等。n階複方陣A的對稱單元互...
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...
在數學中,n 階酉群(unitary group)是 n×n酉矩陣組成的群,群乘法是矩陣乘法。酉群記作 U(n),是一般線性群 GL(n, C) 的一個子群。 在最簡單情形 n ...
厄米特矩陣(Hermitian Matrix,又譯作“埃爾米特矩陣”或“厄米矩陣”),指的是自共軛矩陣。矩陣中每一個第i行第j列的元素都與第j行第i列的元素的共軛相等。...
矩陣範數(matrix norm)是數學中矩陣論、線性代數、泛函分析等領域中常見的基本概念,是將一定的矩陣空間建立為賦范向量空間時為矩陣裝備的範數。套用中常將有限維賦...
么正矩陣表示的就是厄米共軛矩陣等於逆矩陣。對於實矩陣,厄米共軛就是轉置,所以實正交表示就是轉置矩陣等於逆矩陣。實正交表示是么正表示的特例。...
酉變換(unitary transformation)是指酉空間V的等度量變換。對∀α,β∈V,滿足條件(σ(α),σ(β))=(α,β)的線性變換σ稱為酉變換。對n維酉空間V的每一...
廣義逆矩陣對於奇異矩陣甚至長方矩陣都存在、具有通常逆矩陣的一些性質、當矩陣非奇異時,它還原到通常的逆矩陣,滿足其3條性質的矩陣叫做廣義逆矩陣。...
《矩陣理論及方法》是2012年科學出版社出版的圖書,作者是謝冬秀、雷紀剛、陳桂芝。本書主要介紹了工程實際中有套用價值的矩陣理論與方法。...
定義 設A∈Cˇ(n*n),則存在U∈Uˇ(n*n) (這裡,Uˇ(n*n) 表示n階酉矩陣的集合),使得 A=URU℡(U℡為U的共軛轉置) 其中,R為對角線是A的特徵值...
一個方陣A是斜埃爾米特矩陣或反埃爾米特矩陣(Skew-Hermitian or Antihermitian Matrix),如果它的共軛轉置A*是它的負數。即:A是方陣對A的每一個元素,均有:...
《矩陣分析》是2005年機械工業出版社出版的圖書,由(美)合恩(Horn.R.A.)創作,楊奇翻譯。該書是一本對數值計算研究人員來說標準的參考書。本書從數學分析的角度...
《矩陣分析與套用》是2004年9月1日清華大學出版社出版的一本圖書,作者是張賢達。本書將矩陣的分析分為梯度分析、奇異值分析、特徵分析、子空間分析與投影分析五大...
矩陣完備化,又稱矩陣填充(英文為Matrix completion)。其定義為:對於一個元素缺失的矩陣,通過對其有效位置的元素進行採樣,進而恢復出缺失的元素。...
《矩陣分析與計算》 是國防工業出版社出版的圖書,作者是朱元國。本書主要介紹了矩陣論有關基礎理論,同時,引入矩陣計算的相關內容。...
如果範數║·║滿足║A║=║UAV║對任何矩陣A以及酉矩陣U,V成立,那么這個範數稱為酉不變範數。容易驗證,2-範數和F-範數是酉不變範數。因為酉變換不改變矩陣的...
奇異值分解(Singular Value Decomposition)是線性代數中一種重要的矩陣分解,奇異值分解則是特徵分解在任意矩陣上的推廣。在信號處理、統計學等領域有重要套用。...
奇異值是矩陣里的概念,一般通過奇異值分解定理求得。設A為m*n階矩陣,q=min(m,n),A*A的q個非負特徵值的算術平方根叫作A的奇異值。奇異值分解是線性代數和...
三角形陣(在某些情形下為類三角形陣);TZtrapezoidal,梯形陣;UN(complex)unitary,(複數)酉矩陣;UP(complex)unitary,packedstorage,(複數)壓縮儲存的酉矩陣 [2] ...
