基本介紹
- 中文名:奇異值
- 外文名:singular value
- 學科:數學
- 常用於:壓縮;降噪
- 方法:奇異值分解
- 套用:信號處理等
分解定理
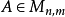
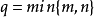
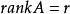
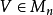
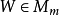
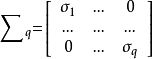
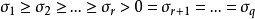

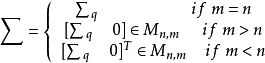
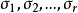
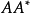
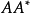
定義
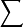
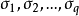
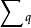
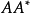
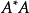
奇異值與秩
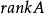
定理及結論
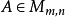
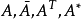
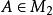
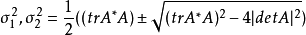
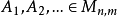
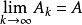
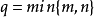
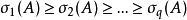
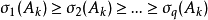
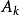
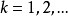
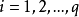
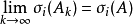
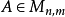
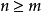
Matlab函式
套用
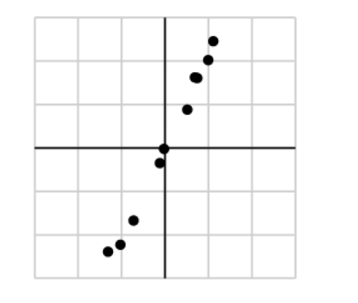
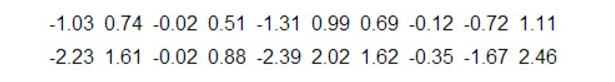
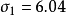
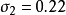

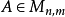
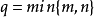
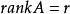
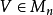
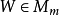
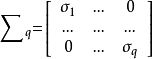
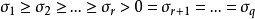

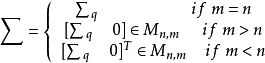
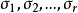
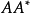
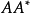
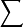
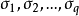
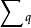
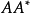
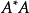
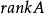
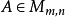
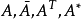
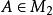
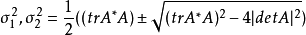
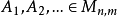
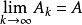
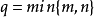
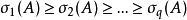
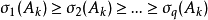
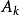
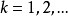
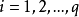
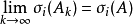
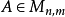
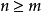

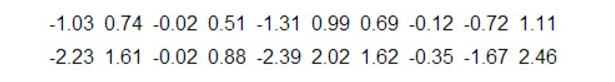
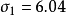
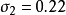

奇異值是矩陣里的概念,一般通過奇異值分解定理求得。設A為m*n階矩陣,q=min(m,n),A*A的q個非負特徵值的算術平方根叫作A的奇異值。奇異值分解是線性代數和...
奇異值分解(Singular Value Decomposition)是線性代數中一種重要的矩陣分解,奇異值分解則是特徵分解在任意矩陣上的推廣。在信號處理、統計學等領域有重要套用。...
矩陣奇異值(singular value of a matrix),是關於mXn階矩陣的一個重要數量。...... 矩陣奇異值(singular value of a matrix),是關於mXn階矩陣的一個重要數量。...
奇異矩陣是線性代數的概念,就是該矩陣的秩不是滿秩。首先,看這個矩陣是不是方陣(即行數和列數相等的矩陣。若行數和列數不相等,那就談不上奇異矩陣和非奇異...
奇異值分解(Singular value decomposition)奇異值分解是線性代數中一種重要的矩陣分解,在信號處理、統計學等領域有重要套用。奇異值分解在某些方面與對稱矩陣或Hermite...
《奇異值分解及其在廣義逆理論中的套用》是2008-05-01科學出版社出版的圖書,作者是 郭文彬,魏木生...
因此,研究全連續運算元A的特徵值和奇異值(即A*A的特徵值的平方根)就是重要的工作。設 A,B是兩個希爾伯特空間上的全連續運算元,Sk(A)表示A的第K個奇異值,則有...
║A║2 = A的最大奇異值 = (max{ λi(AH*A) }) 1/2 (譜範數,即A^H*A特徵值λi中最大者λ1的平方根,其中AH為A的轉置共軛矩陣);...
U和V中分別是A的奇異向量,而B是A的奇異值。AA'的特徵向量組成U,特徵值組成B'B,A'A的特徵向量組成V,特徵值(與AA'相同)組成BB'。因此,奇異值分解和特徵值...
矩陣分解 (decomposition, factorization)是將矩陣拆解為數個矩陣的乘積,可分為三角分解、滿秩分解、QR分解、Jordan分解和SVD(奇異值)分解等,常見的有三種:1)三角...
線上性代數的領域裡,奇異值分解(SVD)將一個大的矩陣拆解成三個小的矩陣。正常的情況下,將奇異值分解(Singular Value Decompositiob, SVD)套用在一個m×n複數...
,n。則稱特徵值的絕對值的最大值為A的譜半徑,記為ρ(A)。 注意要將譜半徑與譜範數(2-範數)區別開來,譜範數是指A的最大奇異值,即A^H*A最大特徵值的...
