雙曲線性映射亦稱雙曲線性同構,是沿一個方向擴張,沿另一個方向收縮的可逆線性映射。線性映射的雙曲性經過小擾動之後不至於被破壞,這一性質在動力系統結構穩定性的研究中起著重要的作用。皮尤夫(Pugh,C.)於1969年進一步證明的結論成為哈特曼定理泛函分析方法證明的核心。
基本介紹
- 中文名:雙曲線性映射
- 外文名:hyperbolic linear map
- 適用範圍:數理科學
簡介
雙曲集


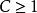




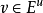







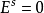

雙曲線性映射亦稱雙曲線性同構,是沿一個方向擴張,沿另一個方向收縮的可逆線性映射。線性映射的雙曲性經過小擾動之後不至於被破壞,這一性質在動力系統結構穩定性的研究中起著重要的作用。皮尤夫(Pugh,C.)於1969年進一步證明的結論成為哈特曼定理泛函分析方法證明的核心。


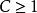




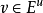







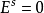
雙曲線性映射亦稱雙曲線性同構,是沿一個方向擴張,沿另一個方向收縮的可逆線性映射。線性映射的雙曲性經過小擾動之後不至於被破壞,這一性質在動力系統結構穩定性的...
這方面典型的例子是托姆的環面雙曲自同構.對二維環面來說,它的定義如下:在平面Rz上給出一個線性映射A:RZ-}RZ,A的矩陣為A有如下特徵:1.在A或A-,的作用...
雙曲線性向t場(hyperbolic linear vertorfields)線性場空間中結構穩定的一類線性向量場.設(E,}}·}})是巴拿赫空間,A: E->E是線性映射.若A的譜集與複平面上...
2雙曲線性映射3雙曲線性映射的擾動4雙曲線性映射的譜第八章Hartman定理1雙曲線性映射的Lipschitz小擾動2Hartman線性化定理3雙曲不動點的局部穩定性...
《動力系統入門教程及最新發展概述》包含兩部分內容:第一部分是入門教程,主要介紹動力系統基本知識,作者通過對壓縮映射、線性系統、簡單二次映射、低維保守系統、彈子...
a引理(a-lemma)亦稱傾角引理,描述系統在雙曲不動點鄰近動力行為的幾何屬性.設f是R ",中。的一鄰域Y的C'微分同胚,以。為雙曲不動點.考慮雙曲線性映射A=Df...
1.1.2映射21.1.3函式21.1.4函式的圖形31.1.5初等函式71.1.6其他函式的例子8*1.1.7雙曲函式及反雙曲函式簡介101.2極限11...
編輯 高等數學,線性代數, 機率統計,複變函數等 [1] 李永群學術成果 編輯 李永群...5. 關於Klein 群與擬共形映射相關性質的研究, 國家自然科學基金,2008年1月至...
藉此,還創建性地提出了求解一般流通量間斷雙曲守恆律方程的δ-映射算法,使其能與任意的經典格式(如WENO和DG)結合,適於其它很多套用問題(如非均質固體彈性波)的...
