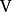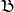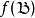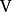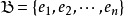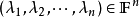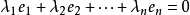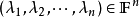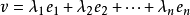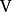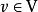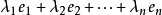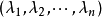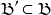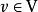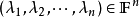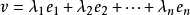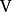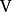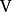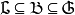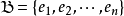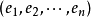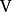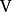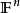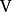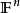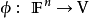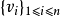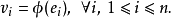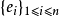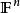基向量

在線性代數中，基(basis)（也稱為基底）是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集，基的元素稱為基向量。

基本介紹

• 中文名：基向量
• 外文名：base vector
• 定義：基的元素稱為基向量
• 相關術語：單位向量
• 領域：數學
• 套用學科：線性代數

簡述

在線性代數中，基(basis)（也稱為基底）是描述、刻畫向量空間的基本工具。向量空間的基是它的一個特殊的子集，基的元素稱為基向量。向量空間中任意一個元素，都可以唯一地表示成基向量的線性組合。如果基中元素個數有限，就稱向量空間為有限維向量空間，將元素的個數稱作向量空間的維數。

使用基底可以便利地描述向量空間。比如說，考察從一個向量空間 射出的線性變換f，可以查看這個變換作用在向量空間的一組基 上的效果。掌握了 ，就等於掌握了 f對 中任意元素的效果。

不是所有空間都擁有由有限個元素構成的基底。這樣的空間稱為無限維空間。某些無限維空間上可以定義由無限個元素構成的基。如果承認選擇公理，那么可以證明任何向量空間都擁有一組基。一個向量空間的基不止一組，但同一個空間的兩組不同的基，它們的元素個數或勢（當元素個數是無限的時候）是相等的。一組基裡面的任意一部分向量都是線性無關的；反之，如果向量空間擁有一組基，那么在向量空間中取一組線性無關的向量，一定能將它擴充為一組基。在內積向量空間中，可以定義正交的概念。通過特別的方法，可以將任意的一組基變換成正交基乃至標準正交基。

定義

給定一個向量空間 。 的一組基B是指 裡面的可線性生成 的一個線性無關子集。B的元素稱為基向量。

更詳細來說，設是在係數域F（比如實數域R或複數域C）上的向量空間V的有限子集。如果滿足下列條件：

對任意，如果，則必然；

對任意，可以選擇，使得。

就說B是向量空間 的一組基。第二個條件中，將一個向量表示成的形式，稱為向量 v在基底下的分解。稱為向量v在基底B下的分量表示。

有有限基的向量空間叫做有限維的空間。要處理無限維的空間，必須把上述基的定義推廣為包括無限的基集合。如果向量空間V的一個子集 (有限或無限B滿足：

它的所有有限子集滿足上面的第一個條件（即線性無關）；

對任意，可以選擇，以及，使得。

就稱B是無限維空間 的一組基。

沒有裝備拓撲結構的向量空間的結構不足以談論向量的無限和，因此上述定義只包括對有限個向量求和。

性質

設B是向量空間 的子集。則B是基，若且唯若滿足了下列任一條件：

是B的極小生成集，就是說只有B能生成 ，而它的任何真子集都不能生成全部的向量空間。

B是 中線性無關向量的極大集合，就是說B在 中是線性無關集合，而且 中沒有其他線性無關集合包含它作為真子集。

中所有的向量都可以按唯一的方式表達為B中向量的線性組合。如果基是有序的，則在這個線性組合中的係數提供了這個向量關於這個基的坐標。

如果承認良序定理或任何選擇公理的等價物，那么作為推論，可以證明任何的向量空間都擁有一組基。（證明：良序排序這個向量空間的元素。建立不線性依賴於前面元素的所有元素的子集。它就是基）。反過來也是真的。一個向量空間的所有基都擁有同樣的勢（元素個數），叫做這個向量空間的維度。這個結果叫做維度定理，它要求系統承認嚴格弱形式的選擇公理即超濾子引理。

例子

• 考慮所有坐標 (a,b)的向量空間R，這裡的a和b都是實數。則非常自然和簡單的基就是向量e₁= (1,0)和e₂= (0,1):假設v= (a,b)是R中的向量，則v=a(1,0) +b(0,1)。而任何兩個線性無關向量如 (1,1)和(−1,2)，也形成R的一個基。
  
• 更一般的說，給定自然數n。n個線性無關的向量e₁,e₂, ...,e_n可以在實數域上生成R。因此，它們也是的一個基而R的維度是n。這個基叫做R的標準基。
  
• 設V是由函式e和e生成的實數向量空間。這兩個函式是線性無關的，所有它們形成了V的基。
  
• 設R[x]指示所有實數多項式的向量空間；則 (1, x, x, ...)是R[x]的基。R[x]的維度因此等於aleph-0。
  

基的擴張

如上所述，一個向量空間的每一組基都是一個極大的線性無關集合，同時也是極小的生成集合。可以證明，如果向量空間擁有一組基，那么每個線性無關的子集都可以擴張成一組基（也稱為基的擴充定理），每個能夠生成整個空間的子集也必然包含一組基。特別地，在任何線性無關集合和任何生成集合之間有一組基。以數學語言來說：如果L是在向量空間 中的一個線性無關集合而集合G是一個包含L而且能夠生成 的集合，則存在 的一組基B，它包含了L而且是G的子集：。

以上兩個結論可以幫助證明一個集合是否是給定向量空間的基。如果不知道某個向量空間的維度，證明一個集合是它的基需要證明這個集合不僅是線性無關的，而且能夠生成整個空間。如果已知這個向量空間的維度（有限維），那么這個集合的元素個數必須等於維數，才可能是它的基。在兩者相等時，只需要證明這個集合線性無關，或這個集合能夠生成整個空間這兩者之一就夠了。這是因為線性無關的子集必然能擴充成基；而這個集合的元素個數已經等於基的元素個數，需要添加的元素是0個。這說明原集合就是一組基。同理，能夠生成整個空間的集合必然包含一組基作為子集；但假如這個子集是真子集，那麼元素個數必須少於原集合的元素個數。然而原集合的元素個數等於維數，也就是基的元素個數，這是矛盾的。這說明原集合就是一組基。

有序基和坐標

基底是作為向量空間的子集定義的，其中的元素並不按照順序排列。為了更方便相關的討論，通常會將基向量進行排列。比如說將： 寫成有序向量組： 。這樣的有序向量組稱為有序基。在有限維向量空間和可數維數的向量空間中，都可以自然地將基底表示成有序基。在有序基下，任意的向量都可以用確定的數組表示，稱為向量的坐標。例如，在使用向量的坐標表示的時候習慣談論“第一個”或“第二個”坐標，這只在指定了基的次序前提下有意義。在這個意義下，有序基可以看作是向量空間的坐標架。

設 是在域F上的n維向量空間。在 上確定一個有序基等價於確定一個從坐標空間到 的一個選定線性同構。

證明：這個證明利用了的標準基是有序基的事實。

首先假設

是線性同構。可以定V的一組有序基如下：

其中的是的標準基。

反過來說，給定一個有序基，考慮如下定義的映射

• φ(x) =x₁v₁+x₂v₂+ ... +x_nv_n,
  

這裡的x=x₁e₁+x₂e₂+ ... +x_ne_n是F的一個元素。不難檢查出φ是線性同構。

這兩個構造明顯互逆。所以V的有序基一一對應於線性同構F→V。

確定自有序基{v_i}線性映射φ的逆映射為V裝備了坐標：如果對於向量v∈V,φ(v) = (a₁,a₂,...,a_n) ∈F，則a_j=a_j(v)的分量是v的坐標，在v=a₁(v)v₁+a₂(v)v₂+ ... +a_n(v)v_n的意義上。

從向量v到分量a_j(v)的映射是從V到F的線性映射，因為φ是線性的。所以它們是線性泛函。它們形成V的對偶空間的基，叫做對偶基。