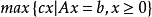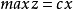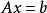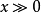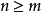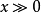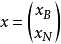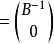基可行解

基可行解即基本可行解的簡稱，是處理線性規劃的基本概念。滿足非負條件的基本解稱為基可行解。

基本介紹

• 中文名：基可行解
• 外文名：basic feasible solution
• 類別：運籌學
• 相關定義：可行解、基、基本解、可行基

基可行解(basic feasible solution)是指，線上性規劃問題中滿足非負約束條件的基解。線性規劃問題如果有可行解，則必有基可行解。

定義

LP問題（線性規劃問題）：或

V: （1）

s.t.

（2）

（3）

若rank(A,b)=rank(A)=m,且,則,其中rank(B)=m.

這樣Ax=b可化為

（2）^’

其中滿足（2）（3）的x稱為可行解，（2）’中稱B為LP的一個基，其列向量稱為基向量

（2）中稱x_B為基變元，x_N為非基變元（關於基B的）

則滿足的基本解稱為基可行解（關於基B的）

其中基本解是指由（2）’，有,此時。若,則稱x為LP的基本解。

由於基本解,則若且唯若時，此基本解為基可行解（它對應可行域的頂點）

此時，基本解中基變元皆取正值者此解為非退化的；否則（基變元有0者）稱為退化的，顯然當，此基可行解是非退化的，否則為退化的。

性質

1. 可行解是基可行解的充要條件是它的正分量所對應的A中列向量線性無關。
2. x是基可行解的充要條件是x是可行域D的頂點。
3. 一個標準形式的LP問題，若有可行解，則至少有一個基可行解。
4. 若標準形式的LP問題有有限的最優值，則一定存在一個基可行解是最優解。
   或敘述為：若標準形式的LP問題的目標函式有有限的最優值，則必可在某個基可行解處達到

套用

3. 4.兩個定理具有重要意義，這兩個定理一起被稱為線性規劃的基本定理。它告訴我們，求解標準形式的LP問題，只需在基可行解的集合中進行搜尋（如果其目標函式有最優值的話），而基可行解的個數是有限的。單純形法就是根據線性規劃的基本定理，給出一定的規律和步驟，在基可行解的一個子集合中逐步搜尋，最終求得最優解或判別問題無最優解。