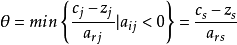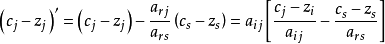定律定義
對偶單純形方法(dualsimplexmethod)純形方法的一種對稱變形.對於原單純形方法而言,在疊代過程中始終保持相應的解對原問題是可行的,並不斷改善對偶問題解(即判別係數)的可行性,直至可行.而對偶單純形方法則是始終保持對偶問題的解的可行性,並不斷改善原問題解的可行性,直至滿足原問題。
方法思路
所謂滿足對偶可行性,即指其檢驗數滿足最優性條件。只要保持檢驗數滿足最優性條件前提下,一旦基解成為可行解時,對偶問題和原問題均可行,由
強對偶性證明,二者均有最優解。
設原始問題的標準形式為max{cx|Ax=b,x≥0},則其對偶問題(Dual Problem)為 min{y
b|y
A≤c}。當原問題的一個基解滿足最優性條件時,其檢驗數小於等於0,當σ=c
j-z
j=c
j-C
BB
-1A≤0時,既有
或
,即知單純形運算元y=C
BB
-1為對偶問題的可行解。換而言之,只要保證檢驗數σ≤0,則對偶問題一定存在可行基B。
在初始單純形表中,一般此可行基B都為單位矩陣I,這時候只要能夠保持檢驗數持續小於等於0疊代下去,通過變換到一個相鄰的目標函式值較小的基可行解(因為對偶問題是求目標函式極小化),並循環進行,一到XB=B-1b≥0時,原問題也為可行解。這時,對偶問題和原問題均為可行解,而且兩者的可行解就是最優解,這就是對偶單純形法求解線性規劃的基本思路。
一旦最終基變數XB≥0,原問題也滿足最優解條件的原因是:對偶問題的最終單純形表中的基變數XB=B-1b和原問題的最終單純形表中的檢驗數的相反數CBB-1取值相等,不難觀察到原問題的檢驗數σ=cj-zj-CBB-1=-B-1b≤0,其檢驗數滿足最優性條件。(註:這裡的B並不是同一個矩陣,它們是各自問題的初始可行基,但CB和b在本質上是同一個向量。)
雖然,本方法借鑑了對偶理論的思路,但是它是求解原問題而非對偶問題的一個方法。而且,一般用對偶單純形法解決的是原始問題是極小化問題,min{cx|Ax=b,x≥0},但是只要先標準化為max{cx|Ax=b,x≥0}即於上面一致。
計算步驟
1.做出單純形表
存在一個對偶問題的可行基B,不妨設B=(P1,P2,···,Pm),列出它的初始單純形表。
CB | 基 | b | x1 | ··· | xr | ··· | xm
| xm+1 | ··· | xs | ··· | xn |
c1 | x1 | b1 | 1 | ··· | 0 | ··· | 0 | a1,m+1 | ··· | a1s | ··· | a1n |
... | ... | ... | ... | | ... | | ... | ... | | ... | | ... |
cr | xr | br | 0 | ... | 1 | ... | 0 | ar,m+1 | ... | ars | ... | arm |
... | ... | ... | ... | | ... | | ... | ... | | ... | | ... |
cm | xm | bm | 0 | ... | 0 | ... | 1 | am,m+1 | ... | ams | ... | amn |
cj-zj | 0 | ... | 0 | ... | 0 | cm+1-zm+1 | | cs-zs | ... | cn-zn |
表中必須有的最後一行的檢驗數σj=cj-zj≤0(j=1,···,n),bi=(i,···,m)的值要求為部分為負數。當對i=1,m,有bi≥0時,即表中原問題和對偶問題均為最優解。否則,通過變化一個基變數,找出原問題的一個目標函式值較小的相鄰基解。
2.確定換出基的變數(離基變數)
因為總存在<0的bi,選取數值最小的作為為第r行,令br=min{bi},其對應變數xr為換出基的變數。
3.確定換入基的變數(入基變數)
(1)為了使下個表中第r行基變數為正值,只有對應的arj<0(j=m+1,···,n)的非基變數才可以考慮作為換入基的變數。為了消除原問題的基解不可行性,變換後的b應該變成正數,故能夠成為主元素arj的應該小於零,意味著這第r行的凡是為非負的元素在判別的是否為主元素時不必考慮。
(2)為了使下一個表中的對偶問題的解仍為可行解,選取檢驗數與對應變數a
rj中的比值最小的那個變數作為主元素,令
。如果有多個值時任選其一。
其中,稱為ars為主元素,主元素對應的那一列的變數xs為換入基的變數。如果aij≥0對於所有的非基變數xj成立,則問題沒有可行解。
3.用換入變數替換換出變數,得到一個新的基。
對新的基再檢查是否所有bi=(i,···,m)≥0。如是,則找到了兩者的最優解,如為否,則返回到第一步再循環進行。
推導過程
分為兩者情況討論滿足最小比值法時選取主元素時,可以保證一個表中的檢驗數為(cj-zj)≤0(對j=1,···,n)
設下一個表中的檢驗數為(cj-zj)',有:
(a)對arj≥0,因cj-zj≤0,故(cj-zj)/arj≤0,主元素ars≤0,(cs-zs)/arj≥0,由此可知方括弧內的值≤0,故有(cj-zj)'≤0。
(b)對arj<0,因[(cj-zj)/arj-(cs-zs)/arj]>0,故有(cj-zj)≤0。
優缺點
對偶單純形法的優點: 不需要人工變數;
當變數多於約束時,用對偶單純形法可減少疊代次數;
在靈敏度分析中,有時需要用對偶單純形法處理簡化。
對偶單純形法缺點: 在初始單純形表中對偶問題是基可行解,這點對多數線性規劃問題很難做到。 因此,對偶單純形法一般不單獨使用