若原始問題(對偶問題)有一個確定的最優解,那么對偶問題(原始問題)也有一個確定的最優解,而且這兩個最優解所對應的目標函式值相等,這就是強對偶性。
基本介紹
- 中文名:強對偶性
- 外文名:strong duality property
- 所屬學科:數學
- 所屬問題:運籌學(線性規劃的對偶理論)
- 相關概念:線性規劃,最優解,目標函式等
強對偶性定理
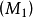



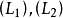
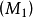


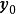


定理證明

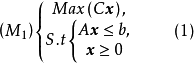
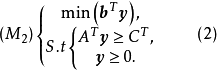
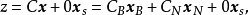

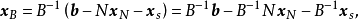
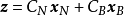

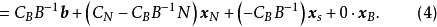
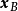

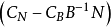

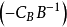
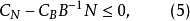
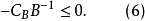
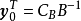


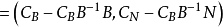

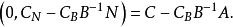
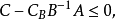
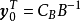
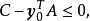
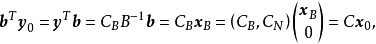

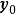


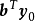
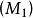
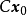
線性規劃的對偶理論

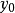
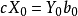

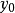
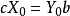
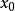
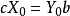
原始問題 | 對偶問題 |
有最優解 | 有最優解 |
有可行解,無有界最優解 | 無可行解 |
無可行解 | 有可行解,無有界最優解 |
無可行解 | 無可行解 |
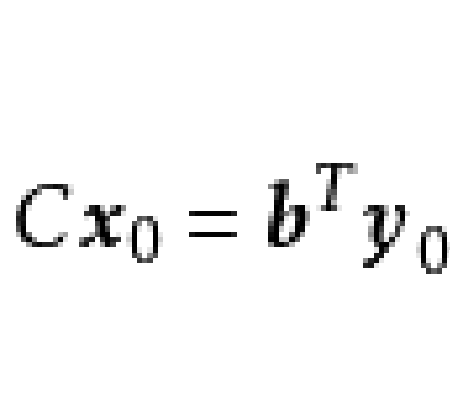
若原始問題(對偶問題)有一個確定的最優解,那么對偶問題(原始問題)也有一個確定的最優解,而且這兩個最優解所對應的目標函式值相等,這就是強對偶性。
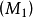



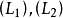
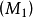


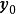



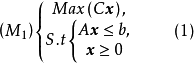
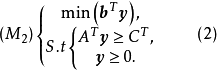
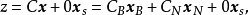

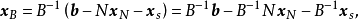
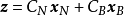

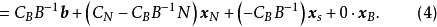
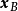

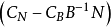

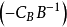
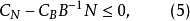
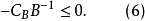
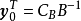


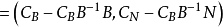

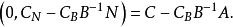
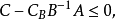
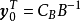
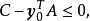
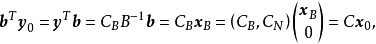

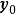


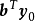
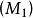
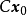

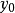
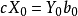

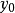
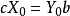
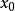
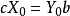
原始問題 | 對偶問題 |
有最優解 | 有最優解 |
有可行解,無有界最優解 | 無可行解 |
無可行解 | 有可行解,無有界最優解 |
無可行解 | 無可行解 |
若原始問題(對偶問題)有一個確定的最優解,那么對偶問題(原始問題)也有一個確定的最優解,而且這兩個最優解所對應的目標函式值相等,這就是強對偶性。...
對偶性是描述導致相同的物理結果,表面上不同的理論之間的對應關係。這種對應關係在信號與系統理論中主要體現在函式x(t)的傅立葉變換X(jw)和函式X(t)的傅立葉...
對偶理論強對偶定理 若上述原始問題和對偶問題都可行,則它們分別有最優解x*和y*,且cx*=y*b。 [2] 對偶理論最優準則定理 若上述原始問題和對偶問題分別有可行...
對偶問題是實質相同但從不同角度提出不同提法的一對問題。對偶現象是許多管理與工程實際中存在的一種普遍現象。例如,企業怎樣充分利用現有人力、物力去完成更多的...
龐特里亞金對偶性定理(Pontryagin dualitytheorem)是關於局部緊交換群與其對偶群的同構定理。...
將∪ 和∩,或者 Ø 和 U 相互交換,一個恆等式就變成了相應的另一個。 這是集合代數的一個非常重要的性質,稱作集合的對偶性原理。它對集合的所有真命題...
模範疇對偶性(duality in categories of modu-les)模範疇等價的對偶概念.設留和酬是兩個範疇,H} : }}}和H": }}}0是兩個逆變函子,若有自然等價II "II'...
在數學中,以亨利·龐加萊(Henri Poincaré)命名的龐加萊對偶性定理是流形結構的基本結果。 它指出,如果M是一個n維定向的閉合流形(緊湊而沒有邊界),則M的第k...
每個線性規劃問題都有一個與之對應的對偶問題。對偶問題是以原問題的約束條件和目標函式為基礎構造而來的。對偶問題也是一個線性規劃問題,因此可以採用單純形法求解。...
凸規劃對偶問題(dual problem of convex pro-gramming)一類綜合的對偶問題.指線性規劃、帶凸性的非線性規劃和二次規劃的對偶問題的綜合形式...
混合型對偶線性規劃(mixed type dual linearprogramming)一類對偶線性規劃(問題).稱是互為混合型對偶線性規劃(問題).[1] 參考資料 1. 數字辭海 ...
分析表明這類模型實際上是Wald模型在非完全競爭市場中的擴展;在第五章和第六章中我們研究了有政府干預的競爭一般均衡的非均衡問題,設計了幾類對偶性模型並利用該...
非線性規劃對偶函式(dual function of nonlinear programming)非線性規劃問題中一種由目標函式和約束函式構成的函式.對於非線性規劃問題...
《國際貿易理論對偶和一般均衡方法》是2011年中國人民大學出版社出版的圖書,作者是美國)阿維納什·迪克西特(Avinash Dixit) (美國)維克多·諾曼(Victor Norman) 。...
非線性規劃對偶問題(dual problem of nonlin-ear programming)與非線性規劃問題相對應的另一非線性規劃問題。對於非線性規劃問題其中L(x,a>是原非線性規劃問題的...
