基本介紹
- 中文名:逆命題
- 外文名:converse proposition
- 領域:數學
- 命題:陳述句可以判斷真假的
- 相關概念:互逆命題、原命題
- 形式:若“結論”則”條件“
定義
命題
互逆命題
逆否命題
互逆命題
形式
逆命題的性質
關係

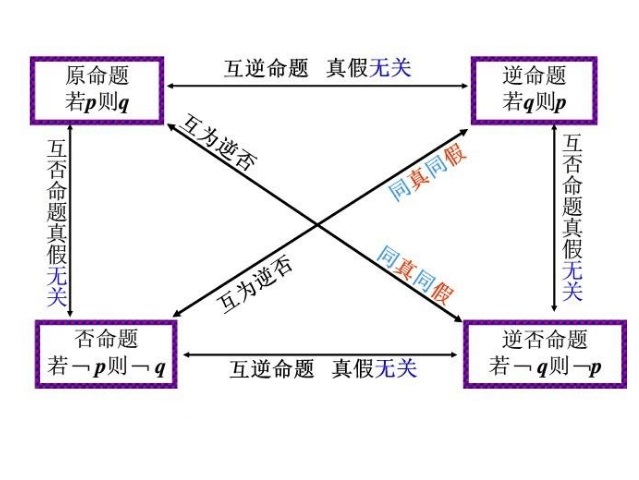
相互關係
真假關係
原命題 | 逆命題 | 否命題 | 逆否命題 |
真 | 真 | 真 | 真 |
真 | 假 | 假 | 真 |
假 | 真 | 真 | 假 |
假 | 假 | 假 | 假 |

原命題 | 逆命題 | 否命題 | 逆否命題 |
真 | 真 | 真 | 真 |
真 | 假 | 假 | 真 |
假 | 真 | 真 | 假 |
假 | 假 | 假 | 假 |
一般的,在數學中把用語言、符號或式子表達的,可以判斷真假的陳述句叫做命題。對於兩個命題,如果一個命題的條件和結論分別是另外一個命題的結論和條件,那么這兩個...
逆定理是將某一定理的條件和結論互換所得命題也是一個定理,那互換之後的定理就是原來定理的逆定理。(即如果一個定理的逆命題能被證明為真命題,那么它叫做原定理...
數學命題(mathematical proposition)是一類重要的命題,一般來講是指數學中的判斷。...... 1. 四種命題的相互關係:原命題與逆命題互逆,否命題與原命題互否,原命題...
原命題2:如果CD是直角三角形ABC斜邊AB上的中線,那么它等於AB的一半。逆命題2:如果線段BD的一端B是直角三角形ABC的頂點,另一端D在斜邊AC上,且BD等於AC的一半,...
注:性質3和4互為逆命題。 5、反演變換φ把任一個不通過反演中心O的圓周變成不能過反演中心O的圓周。(圓→圓) 由於可以把直線看成圓周,上述性質2—5可經綜合...
同一原理(principle of identity)亦稱同一法則,是相對同一概念而顯現的一種關係。一個命題的條件和結論都惟一存在,它們所指的概念是同一概念時,這個命題與其逆...
在符契約一法則的前提下,代替證明原命題而證明它的逆命題成立的一種方法叫做同一法...
夏普爾定理的逆命題也成立。逆定理 設⊙O₁、⊙O₂的半徑分別為r和R,圓心距為d,若 則存在一個△ABC,它外切(或旁切)於⊙O₁,又內接於⊙O₂。...
三線合一逆命題 編輯 ① 如果三角形中有一角的角平分線和它所對邊的高重合,那么這個三角形是等腰三角形。② 如果三角形中有一邊的中線和這條邊上的高重合,...
題設是指兩種命題,第一種是陳述句,第二種是若p,則q”形式的命題。...... 只有第二種命題形式,也就是有題設和結論的命題才有原命題、逆命題、否命題、逆否...
就是說,費馬小定理的逆命題是否成立?對於1<n<300的數來說,計算可知,能整除 的奇數n都是素數,這使得人們在很長的時間內認為費馬小定理的逆命題當然成立。德國...
正多邊形 扇形面積 互否命題 互逆命題 等價命題 尺寸注法標準方程 平移公式 旋轉公式 有向線段 定比分點 有向直線經驗公式 有心曲線 無心曲線 參數方程 普通...
一個簡單定理“等腰三角形兩底角的內角平分線相等”,善於思考的他突然逆向思維,提出上述逆命題是否成立,萊默斯一天、兩天都沒有證明出來,他堅信這個命題是真的,可卻...
里斯-費希爾定理是貝塞爾不等式的逆命題。貝塞爾不等式表明:{ck}為L2[a,b]中某個函式的傅立葉係數的必要條件是{ck}2的和函式收斂,里斯-費希爾定理表明這個條件...
2.若∠1+∠2=180°,則∠1和∠2互為鄰補角 指出命題的逆命題,並判斷真假。答案:原命題錯,鄰補角需要有一條邊重合 .逆命題:若∠1和∠2互為鄰補角,則∠1...
這個定理的一種逆命題由 Anne C. Davis 證明了: 如果所有次序保持函式 f : L → L 有不動點,則 L 是完全格。中文名 克納斯特-塔斯基定理 外文名 ...
