基本介紹
- 中文名:可行域
- 外文名:feasible region
- 所屬學科:數理科學
- 相關概念:線性規劃、可行解、約束條件等
- 別稱:約束區域
基本介紹

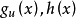


可行域的其他性質
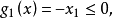


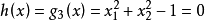

 圖1(a)凸集
圖1(a)凸集 圖1 (b)非凸集
圖1 (b)非凸集 圖1(c)非凸集
圖1(c)非凸集
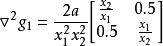
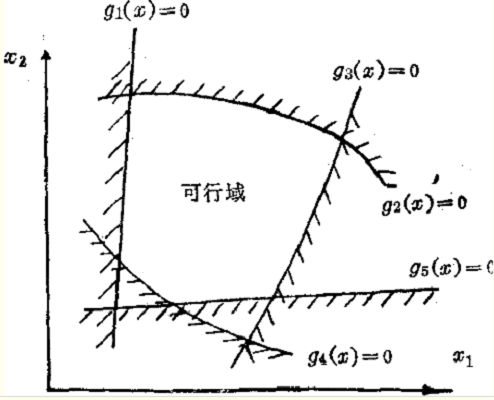

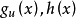


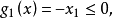


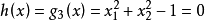

 圖1(a)凸集
圖1(a)凸集 圖1 (b)非凸集
圖1 (b)非凸集 圖1(c)非凸集
圖1(c)非凸集
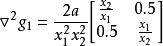
若某項設計有m個不等式約束條件,則由m個約束面在設計空間中形成兩個區域,凡滿足不等式約束方程組的設計變數選擇區域,稱為設計可行域,或稱約束區域;凡不滿足不...
可行方向是求解約束最最佳化問題中,保持可行性的搜尋方向。設f(x),gₑ(x)和hₐ(x)都具有一階連續偏導數,X={x|gₑ(x)≤0(e=1,2,…,p);hₐ(x...
可行基線上性代數中也叫可行解,滿足某線性規劃所有的約束條件(指全部前約束條件和後約束條件)的任意一組決策變數的取值,都稱為該線性規劃的一個可行解,所有可行解...
設X是非線性規劃問題(NLP)的一個可行點,非零矢量P即是點X處的可行方向,又是f(X)在點X處的一個下降方向,則稱P為f(x)在點X處的一個可行下降方向。 ...
滿足某線性規劃所有的約束條件(指全部前約束條件和後約束條件)的任意一組決策變數的取值,都稱為該線性規劃的一個可行解,所有可行解構成的集合稱為該線性規劃的可行...
基可行解即基本可行解的簡稱,是處理線性規劃的基本概念。滿足非負條件的基本解稱為基可行解。...
基本可行解(basic feasible solution)亦稱可行點或允許解,是線性規劃的重要概念。線上性規劃問題中,滿足非負約束條件的基本解,稱基本可行解,簡稱基可行解。線性規劃...
圖解法一般是指求解僅含兩個變數的線性規劃問題的一種方法。只含兩個變數的線性規劃問題,由約束條件確定的可行域可以在二維平面上表示出來,按照一定規則,在可行域...
起作用約束(active constraint)亦稱緊約束或積極約束,是指在某可行點處使不等式約束成為等式的約束。對於可行點x',當gi(x')=0時點x'處於這個約束形成的可行域...
(1)為什麼斜率-A/B>0時,直線Ax+By+C=0上方可行域的〈所有計算點(x1,y1)〉令直線Ax1+By1+C<0,直線Ax+By+C=0下方可行域〈所有計算點(x2,y2)〉令...
所表示的幾何面或線將設計空間分成兩部分:一部分中所有設計均滿足所有的約束條件,這部分空間稱為設計點的可行域;另一部分所有點均不滿足約束條件,稱為設計點的不...
內部罰函式法也稱為障礙罰函式法,這種方法是在可行域內部進行搜尋,約束邊界起到類似圍牆的作用,如果當前解遠離約束邊界時,則罰函式值是非常小的,否則罰函式值接近...
如果不等式g(x)滿足條件g(x)=0,則這個約束條件稱為點x的積極約束。任意一個等式約束條件都是可行域內所有點的積極約束。詞條標籤: 文化術語 , 文化, 學科 ...
目標函式是線性的,求目標函式的最大值或最小值.熟悉線性約束條件(不等式組)的幾何表征是平面區域(可行域).體會可行域與可行解、可行域與最優解、可行解與最優...
無解性,也叫做無可行解性,是指線上性規劃問題中,使得可行域為空集的性質。...... 無解性,也叫做無可行解性,是指線上性規劃問題中,使得可行域為空集的性質。...
無風險證券對有效邊界的影響是:(幾何特徵)現有證券組合可行域較之原有風險證券組合可行域擴大並具有直線邊界。原因:1、投資者通過將無風險證券F與每個可行的風險...
從圖解法可以直觀地看到可行域和最優解的幾何意義:所有可行解構成的集合是凸集,也可能為無界域;它們有有限個頂點,線性規劃問題的每個基可行解對應可行域的一個頂點...
