基本介紹
- 中文名:約束最佳化問題
- 主要起源:實際問題是包含約束條件的
- 具體形式:min f(x)
- 滿足約束條件:g(x)<=0h(x)=0
方程一般形式
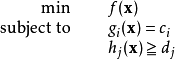



約束 (數學)
效用
歷史
- 最大效用原理:在風險和不確定條件下,個人的決策行為準則是為了獲得最大期望效用值而非最大期望金額值。
效用的基數性和序數性
相關條目
- 拉格朗日乘數
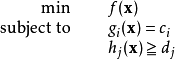



約束最佳化問題(亦譯為受約束的最最佳化問題)是一類數學最最佳化問題,它由目標函式以及與目標函式中的變數相關的約束條件兩部分組成,最佳化過程則為在約束條件下最最佳化(最...
約束最最佳化問題(constrained optimization problem)是指具有約束條件的非線性規劃問題。僅有等式約束條件的約束最最佳化問題,可採用消元法、拉格朗日乘子法或罰函式法,將...
約束最佳化(Constrained Optimization),即約束最佳化問題,是最佳化問題的分支。它是在一系列約束條件下,尋找一組參數值,使某個或某一組函式的目標值達到最優。其中約束...
約束最佳化法(Constrained Optimization Method):約束最佳化問題是在自變數滿足約束條件的情況下目標函式最小化的問題,其中約束條件既可以是等式約束也可以是不等式約束。...
最最佳化是套用數學的一個分支,主要指在一定條件限制下,選取某種研究方案使目標達到最優的一種方法。最最佳化問題在當今的軍事、工程、管理等領域有著極其廣泛的套用。...
約束最佳化方法是尋求具有約束條件的線性或非線性規劃問題解的數值算法。假設ƒ(尣),gi(尣)(i=1,2,…,m)是n維歐幾里得空間Rn中的實值函式。所謂約束最佳化問題,...
在數學規劃中,對於決策方案的各項限制,常以不等式或方程式的形式出現。在經濟問題中,對目標函式常常要在一定約束條件下求最大值(或最小值),它們包含著用來代表...
工程設計中最最佳化問題(optimization problem)的一般提法是要選擇一組參數(變數),在滿足一系列有關的限制條件(約束)下,使設計指標(目標)達到最優值。因此,最最佳化...
最最佳化方法,是指解決最最佳化問題的方法。所謂最最佳化問題,指在某些約束條件下,決定某些可選擇的變數應該取何值,使所選定的目標函式達到最優的問題。即運用最新科技...
最最佳化問題根據有無約束條件可以分為無約束條件的最最佳化問題和有約束條件的最最佳化問題。無約束條件的最最佳化問題就是在資源無限的情況下求解最佳目標,而有約束條件的...
對於式(1b)的等式約束,凡是滿足該約束的任一可行點,該等式約束都是起作用約束。由於約束最佳化問題的最優解不僅與目標函式有關,而與約束集合的性質也有關。在可行...
凸最佳化,或叫做凸最最佳化,凸最小化,是數學最最佳化的一個子領域,研究定義於凸集中的凸函式最小化的問題。...
組合最最佳化問題是在給定有限集合的所有具某些特性的子集簇中,尋找使某種指標達到最優的子集的問題。依據問題的性質,包括有排序問題、匹配問題和網路流問題等。組合...
約束極值(constrainted extremum)是多元函式在一定限制條件下的極值。帶有約束條件的極值問題稱為約束極值問題,也叫規劃問題。求解約束極值問題要比求解無約束極值問題...
非線性約束算法、遺傳算法和神經網路算法,以及大型工具軟體包MATLAB中的最最佳化工具...套用本書介紹的基本算法和MATLAB程式,可以方便地求解各類實際的工程設計問題。 [...
《最最佳化問題的擾動分析》是 2010年 科學出版社出版的圖書,作者是 (法)J.F.博南,(美)A.夏皮羅。...
非線性規劃主要介紹非線性規劃的基本概念與基本原理、無約束問題最最佳化方法和約束問題的最最佳化方法;現代最最佳化算法主要介紹計算複雜性與啟發式算法、模擬退火算法、遺傳...
1.3 最最佳化問題的分類1.4 疊代算法及其收斂性1.5 函式的凸性與凸規劃複習思考題習題第2章 無約束最佳化方法2.1 一維搜尋2.2 無約束最佳化的解析法2.3 無約束...
《最佳化與決策》系統地介紹了最佳化和決策的基本理論與問題的基本求解方法。內容包含兩大方面,第一方面介紹最佳化的數學基礎和最優性條件、凸最佳化、線性最佳化、無約束最佳化...
最佳化設計是從多種方案中選擇最佳方案的設計方法。它以數學中的最最佳化理論為基礎,以計算機為手段,根據設計所追求的性能目標,建立目標函式,在滿足給定的各種約束條件下...
最佳化控制是指在給定的約束條件下,尋求一個控制系統,使給定的被控系統性能指標取得最大或最小值的控制。...
約束法(constraint method)一種求解多目標規劃問題的方法.指在多個目標函式中,確定一個主要目標,對其他各目標都給定一個所期望的值,將其轉化為約束條件,從而把多...
