工程設計中最最佳化問題(optimization problem)的一般提法是要選擇一組參數(變數),在滿足一系列有關的限制條件(約束)下,使設計指標(目標)達到最優值。因此,最最佳化問題通常可以表示為數學規劃形式的問題。
基本介紹
- 中文名:最最佳化問題
- 外文名:optimization problem
- 典型例子:目標函式的可行解
- 解決方法:整數規劃
- 動態規劃:最優策略
- 定式:數學規劃
概念
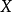


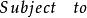




基本原理







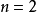
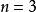



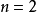

工程設計中最最佳化問題(optimization problem)的一般提法是要選擇一組參數(變數),在滿足一系列有關的限制條件(約束)下,使設計指標(目標)達到最優值。因此,最最佳化問題通常可以表示為數學規劃形式的問題。













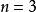



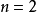
工程設計中最最佳化問題(optimization problem)的一般提法是要選擇一組參數(變數),在滿足一系列有關的限制條件(約束)下,使設計指標(目標)達到最優值。因此,最最佳化...
最最佳化是套用數學的一個分支,主要指在一定條件限制下,選取某種研究方案使目標達到最優的一種方法。最最佳化問題在當今的軍事、工程、管理等領域有著極其廣泛的套用。...
最最佳化方法,是指解決最最佳化問題的方法。所謂最最佳化問題,指在某些約束條件下,決定某些可選擇的變數應該取何值,使所選定的目標函式達到最優的問題。即運用最新科技...
約束最最佳化問題(constrained optimization problem)是指具有約束條件的非線性規劃問題。僅有等式約束條件的約束最最佳化問題,可採用消元法、拉格朗日乘子法或罰函式法,將...
最最佳化模型(optimization model)在經濟管理工作中運用線性規劃、非線性規劃、動態規劃、整數規劃以及系統科學方法所確定的表示最優方案的模型。它能反映經濟活動中的...
線性最最佳化問題( linear optimization problem)見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化...
網路最最佳化問題是一類特殊的組合最最佳化問題。套用圖論理論,通過網路的拓撲結構及其性質,對網路進行研究,並且以計算機算法尋求網路中的最短路、最大流等。...
最最佳化原理也稱最優性原理。指解決多階段決策問題的理論。這個理論是美國的貝爾曼在1956年提出的。它原來的表述是:一個過程的最優策略具有這樣的性質,即無論其初始...
組合最最佳化問題是在給定有限集合的所有具某些特性的子集簇中,尋找使某種指標達到最優的子集的問題。依據問題的性質,包括有排序問題、匹配問題和網路流問題等。組合...
最最佳化理論是關於系統的最優設計、最優控制、最優管理問題的理論與方法。最最佳化,就是在一定的約束條件下,使系統具有所期待的最優功能的組織過程。是從眾多可能的...
隨機最最佳化指帶有隨機因素的最最佳化問題,利用機率統計、隨機過程、隨機分析等工具解決。...
《最最佳化計算方法》是2008年華南理工大學出版社出版的圖書,作者是蔣金山、何春雄、潘少華。...
凸最佳化,或叫做凸最最佳化,凸最小化,是數學最最佳化的一個子領域,研究定義於凸集中的凸函式最小化的問題。...
解析最最佳化方法,也稱間接最最佳化方法,是求解最最佳化問題的一類方法。它要求把所研究的對象用數學表達式描述出來,然後用數學解析方法求出最優解。...
多目標最最佳化問題( multiple objective optimizationproblem)見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上...
排隊系統最最佳化問題是指通過系統設計和控制的最最佳化,達到服務機構成本與顧客等待費用之和最小的辦法。分為兩類:(1)系統設計的最最佳化,稱為靜態問題,從排隊論產生...
非線性最最佳化問題( nonlinear optimizationproblem)見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最...
單目標最最佳化問題(simple objective optimizationproblem)見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說...
無約束最最佳化問題( unconstrained optimizationproblem)見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,...
確定型最最佳化問題見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化是研究在一個給定的集合S上...
隨機型最最佳化問題( stochastic optimizationproblem)見“最最佳化問題”。從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最...
《最最佳化方法與最優控制》是哈爾濱工程大學出版社出版的圖書,作者是王曉陵、陸軍。本書可作為高等工業院校自動化、測控技術與儀器、電氣工程及其自動化等相關專業的...
《 最最佳化理論與方法》是2008年國防工業出版社出版的圖書,作者是傅英定。本書內容包括最最佳化基礎、線性規劃、對偶線性規劃、無約束最最佳化方法、約束最佳化方法、直接...
目錄 1 概述 2 方法分類 3 最佳化策略 4 優勢 5 發展問題 6 意義 搜尋引擎最佳化概述 編輯 搜尋引擎最佳化,又稱為SEO,即Search Engine Optimization,它是一種...
無約束最最佳化方法是求解無約束最最佳化問題的方法,有解析法和直接法兩類。...... 解析法就是利用無約束最最佳化問題中目標函式 f(x) 的解析表達式和它的解析性質(如...
