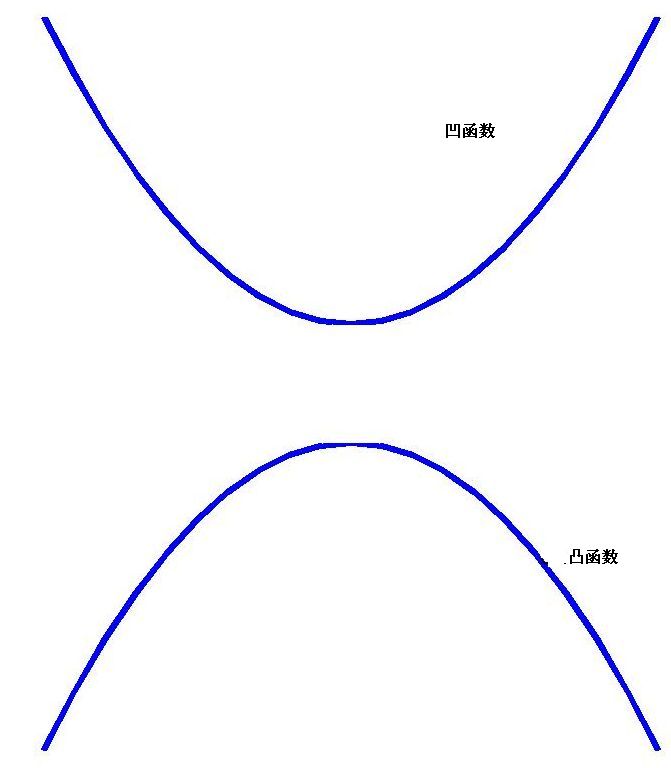
數學模型中的一種，在數學當中，凹函式是凸函式的相反。
凸函式是一個定義在某個向量空間的凸集C（區間）上的實值函式f。設f為定義在區間I上的函式，若對I上的任意兩點X1<X2和任意的實數λ∈（0，1），總有f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2), 則f稱為I上的凹函式。
基本介紹
- 中文名：凹函式
- 外文名： concave function
- 相關領域：數學
- 相關術語：凸函式
- 前提：連續函式
- 別稱：下凸函式
定義,性質,證明,套用舉例,
定義
如果定義在某一區間上的一元實函式是連續函式，且對這一區間中的任何兩點X1、X2，當X1<X2時，有不等式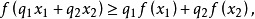
其中q1、q2為正數，q1+q2=1，這時，我們把函式f(x)叫做凹函式，或叫做下凸函式。
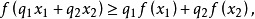
如果把上述條件中的“≥”改成“>”，則叫做嚴格凹函式，或叫做嚴格下凸函式。
如果y=f(x)是(嚴格)凹函式，那么它的圖象是(嚴格)凹曲線，或叫做(嚴格)下凸曲線。
凹函式的概念是詹森(J.L.w.v.Jermen，1859～1925)引入的，他所採取的定義條件是
相當於上述定義中
的特殊情況形。這種定義對於連續函式來說是等價的。
如果f(x)是凹函式，那么-f(x)即是凸函式，通常都是把凹函式轉化為凸函式來研究。
如果一元實函式f(x)在某區間二階可導，那么這一函式為凹函式的充要條件是在這一區間上恆有f‘’(x)小於等於0(對於嚴格凹函式，只要改成f‘’(x)<0就可以了)。
與凸函式（下凸）對比，這裡的凹函式（上凸）應有：如果其二階導數在區間上恆小於等於0，就稱為凹函式。如果其二階導數在區間上恆小於0，就稱為嚴格凸函式。
在數學當中，凹函式是凸函式的相反。
性質
如果一個可微函式f它的導數f'在某區間是單調上升的，也就是二階導數若存在，則在此區間，二階導數是大於零的，f就是凹的；即一個凹函式擁有一個下跌的斜率（當中下跌只是代表非上升而不是嚴謹的下跌，也代表這容許零斜率的存在。）
如果一個二次可微的函式f，它的二階導數f'(x)是正值（或者說它有一個正值的加速度），那么它的圖像是凹的；如果二階導數f'(x)是負值，圖像就會是凸的。當中如果某點轉變了圖像的凹凸性，這就是一個拐點。
如果凹函式（也就是向上開口的）有一個“底”，在底的任意點就是它的極小值。如果凸函式有一個“頂點”，那么那個頂點就是函式的極大值。
如果f(x)是二次可微的，那么f(x)就是凹的若且唯若f''(x)是非正值。如果二階導數是負值的話它就是嚴謹凹函式，但相反而言又不一定正確。
證明
設函式f(x)在定義域內連續可導且滿足f''(x)>0；設x1<x2,0<a<1、證明：f[ax1+(1-a)x2]<af(x1)+(1-a)f(x2)；（即利用凹函式的充要條件來證明其定義。）
因ax1+(1-a)x2-x1=(1-a)(x2-x1)>0；
則x1<ax1+(1-a)x2；
根據拉格朗日中值定理。
必存在x1<μ< ax1+(1-a)x2；
使f[ax1+(1-a)x2]-f(x1)= (1-a)(x2-x1)f'(μ)；
同理。
存在ax1+(1-a)x2<ξ<x2；
使f(x2)- f[ax1+(1-a)x2]= a(x2-x1)f'(ξ)；
故a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}=a (1-a)(x2-x1)[f’(μ)- f’(ξ)]；
根據拉格朗日中值定理。
有μ<δ<ξ；
f'(μ)- f'(ξ)=(μ-ξ)f''(δ)；
因f''(x)>0；
則f'(μ)- f'(ξ)<0；
則a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}<0；
整理後得f[ax1+(1-a)x2]<af(x1)+(1-a)f(x2)；
同理，若f''(x)≤0，則結果相反 。
即若f''(x)≤0，則f[ax1+(1-a)x2]≥af(x1)+(1-a)f(x2)；滿足凹函式的定義。
證明完畢；
注意：中國某些機構關於函式凹凸性定義和國外的定義是相反的。Convex Function在某些中國大陸的數學書中指凹函式。Concave Function指凸函式。但在中國大陸涉及經濟學的很多書中，凹凸性的提法和其他國家的提法是一致的，也就是和數學教材是反的。舉個例子，同濟大學高等數學教材對函式的凹凸性定義與本條目相反，本條目的凹凸性是指其上方圖是凹集或凸集，而同濟大學高等數學教材則是指其下方圖是凹集或凸集，兩者定義正好相反。
套用舉例
線性函式
是En中的凸函式嗎?是En中的凹函式嗎?是En中的嚴格凸函式嗎?是En中的嚴格凹函式嗎?
解：對En中任意兩點X1、X2及0<α<1中每個α，αX1+(1一α)X2也在En中，有
所以f(X)是凸函式，也是凹函式，但不是嚴格凸函式，也不是嚴格凹函式。
