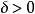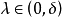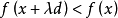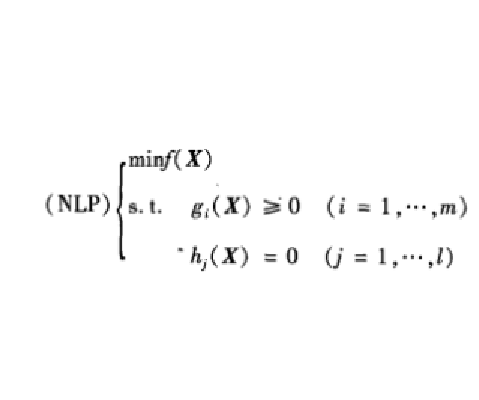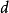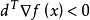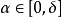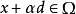可行下降方向

設X是非線性規劃問題(NLP)的一個可行點，非零矢量P即是點X處的可行方向，又是f(X)在點X處的一個下降方向，則稱P為f(x)在點X處的一個可行下降方向。

基本介紹

• 中文名：可行下降方向
• 外文名：feasible descent direction
• 相關問題：非線性規劃問題
• 相關概念：可行方向、可行點、下降方向等

研究問題

對約束最佳化問題（非線性規劃問題NLP）

(1)

記可行集

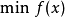
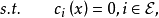
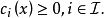
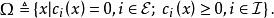
對約束最佳化問題的最優值點，一個顯然的結論是該點在可行域內部不能含有下降方向。

可行下降方向的定義

定義一

若可行方向滿足，則稱d為約束最佳化問題(1)在x點的可行下降方向。

定義二

設X是非線性規劃問題(NLP)的一個可行點，非零矢量d即是點X處的可行方向，又是f(X)在點X處的一個下降方向，則稱d為f(X)在點X處的一個可行下降方向。

可行方向

定義

稱為約束最佳化問題(1)在x點的可行方向，若存在，對任意，有。

可行方向的基本性質

若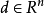為約束最佳化問題(1)在x點的可行方向，則

證明: 由於一個等式約束可以等價地表示成兩個不等式約束，為此，我們只考慮含有不等式約束的情形，若結論不成立，則存在，使得，從而對充分小的有

這與d為約束最佳化問題(1)在x點的可行方向矛盾。 證畢。

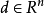
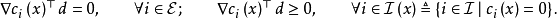
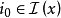
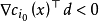
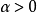
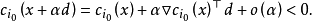
對約束為線性的情況，上述結論的逆命題也成立，藉助可行方向，容易建立約束最佳化問題的下述性質。

相關定理

定理1

設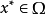是約束最佳化問題(1)的局部最優解，則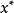點的任一可行方向d滿足。

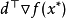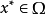
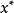
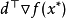
該結論是說，在約束最佳化問題的最優值點不存在可行下降方向。

利用定理1，並結合穩定點的定義，我們可以得到下面的結論：

定理2

若約束最佳化問題(1)的可行域為閉凸集，則其任一局部最優解為其穩定點。

下降方向

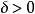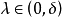定義設x是(NLP)的一個可行點(可行域中的點)，若存在非零矢量d滿足：存在，當時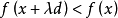，則稱d為f(x)在點x處的一個下降方向。