可行方向是求解約束最最佳化問題中,保持可行性的搜尋方向。設f(x),ge(x)和ha(x)都具有一階連續偏導數,X={x|ge(x)≤0(e=1,2,…,p);ha(x)=0(a=1,2,…,q)},設xº是一個可行點,即xº∈X,對於某一方向p來說,若存在數λ0>0,使對於任意的λ(0≤λ≤λ0)均有xº+λp∈X成立,則p是點xº處的一個可行方向。
基本介紹
- 中文名:可行方向
- 外文名:feasible direction
- 所屬學科:數理科學
- 套用:求解約束最最佳化問題
- 產生條件:可行條件、下降條件
整體介紹,產生可行方向的條件,可行條件,下降條件,可行方向的產生方法,隨機產生法,線性規劃法,梯度投影法,
整體介紹
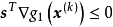
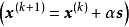
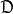


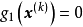

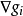
 圖1 可行方向
圖1 可行方向式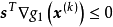 的極限情況是取等號,這時有
的極限情況是取等號,這時有
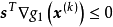
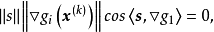

當某個設計點同時有幾個約束起作用時,如圖1中的x點是約束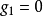 和約束
和約束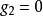 約束面的交點,其可行方向集合
約束面的交點,其可行方向集合
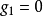
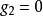
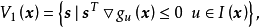
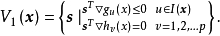
產生可行方向的條件
可行方向是指沿該方向作微小移動後,所得到的新點是可行點,且目標函式值有所下降。顯然,可行方向應滿足可行和下降兩個條件。
可行條件
方向的可行條件是指沿該方向作微小移動後,所得到的新點為可行點。若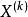 點在一個約束面上,對
點在一個約束面上,對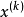 點作約束面
點作約束面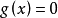 的切線
的切線 ,顯然滿足可行條件的方向
,顯然滿足可行條件的方向 應與起作用的約束函式在
應與起作用的約束函式在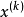 點的梯度
點的梯度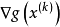 的夾角大於或等於90°。
的夾角大於或等於90°。
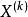
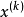
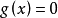


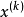
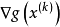
下降條件
方向的下降條件是指沿該方向作微小移動後,所得新點的目標函式值是下降的,滿足下降條件的方向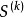 應和目標函式在
應和目標函式在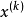 點的梯度
點的梯度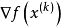 的夾角大於90°。
的夾角大於90°。
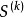
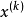
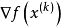
可行方向的產生方法
滿足可行和下降條件的方向在可行下降方向區內,則在該區內尋找一個最有利的方向作為本次疊代的搜尋方向,關於這個方向的產生方法主要有隨機產生法、線性規劃法和梯度投影法幾種,具體方法及過程可參考後文相關參考書籍。
隨機產生法
這種方法從原理上講與隨機方向搜尋法產生的方法基本相同。先在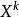 點產生N個隨機單位方向向量
點產生N個隨機單位方向向量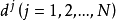 ,然後將產生的N個方向逐個進行可行性和下降條件的檢驗,用這種方法產生適用可行方向的優點是比較簡單,容易實現程式化。
,然後將產生的N個方向逐個進行可行性和下降條件的檢驗,用這種方法產生適用可行方向的優點是比較簡單,容易實現程式化。
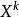
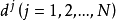
線性規劃法
這種方法對線性和非線性的不等式約束最佳化問題均適應,但不能容納等式約束,是可行方向法中選擇適用可行方向的主要方法之一。這種方法的要點是:在可行下降扇形區內選擇一方向d進行搜尋,可得到一個目標函式值下降的可行點。
梯度投影法
梯度投影法有時也稱為大步梯度法,主要用於求解線性約束最佳化問題。當沿約束面進行尋優搜尋時,需要確定一個沿約束面運動的適用可行方向。


