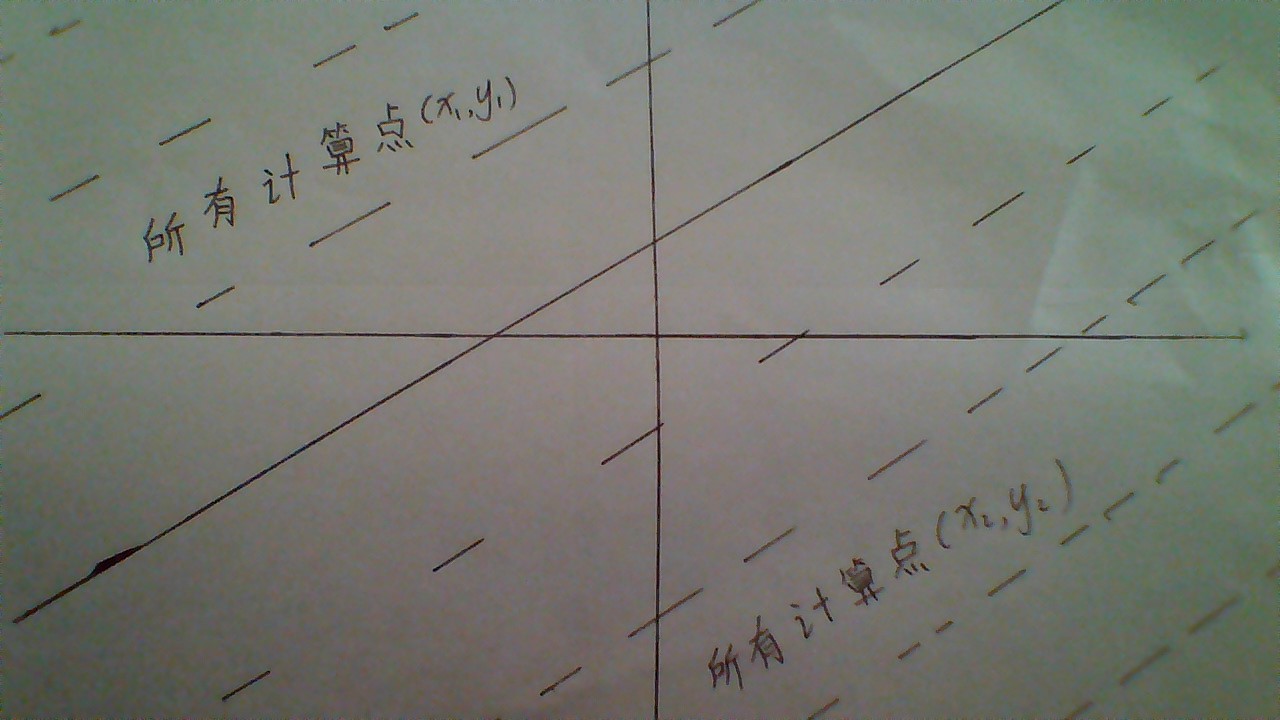
（1）為什麼斜率-A/B>0時，直線Ax+By+C=0上方可行域的〈所有計算點(x1,y1)〉令直線Ax1+By1+C<0，直線Ax+By+C=0下方可行域〈所有計算點(x2,y2)〉令直線Ax2+By2+C>0?
（2）為什麼斜率-A/B<0時，直線Ax+By+C=0上方可行域的〈所有計算點(x3,y3)〉令直線Ax3+By3+C>0。直線Ax+By+C=0下方可行域〈所有計算點(x4,y4)〉令直線Ax4+By4+C<0?
（3）為什麼當斜率=0時,y=C,C為常數。上方可行域的〈所有計算點(x5,y5)〉令直線y>C,下方可行域的〈所有計算點(x6,y6)〉令直線y<C?
（4）為什麼當斜率不存在，x=C,左方可行域的〈所有計算點(x7,y7)〉令直線x<C,右方可行域的〈所有計算點(x8,y8)〉令直線x>C
基本介紹
- 中文名：線性規劃的證明
- 外文名：To prove the linear programming
- 創始人：顏裕傑
- 所屬學科：運籌學
原理：,證明：,
原理：
因為點動成線，線動成面，所以可行域可以看成無數個計算點組成並落在原直線Ax+By+C=0的所有平行線上，又因為平行於Ax+By+C=0的平行線可以知道A與B為定值所以寫成Ax+By+C+ΔC=0，ΔC≠0。要找到可行域令經過可行域的所有平行線Ax+By+C+ΔC=0中可行域令Ax+By+C與0的關係，又因為找出所有平行線中ΔC與0的關係就可以找到可行域令Ax+By+C與0的關係。就可以證明可行域令Ax+By+C的大小與0的關係了。
證明：
（1）∵設直線為Ax+By+C=0,A>0.
∵當斜率
-A/B>0時.
又∵A>0
∴B<0
又∵直線上下方可行域的所有計算點令平行於原直線Ax+By+C=0的所有直線Ax+By+C+△C=0
又∵原直線向上平移時,A和B為定值,因為B<0,又因為-C/B變大為-（C+△C)/B
∴經過分析得:△C>0
又∵Ax1+By1+C+△C=0
∴Ax1+By1+C<0
又∵原直線向下平移時,A和B為定值,因為B<0,又因為-C/B變小為-（C+△C)/B
∴經過分析得:△C<0
又∵Ax2+By2+C+△C=0
∴Ax2+By2+C>0
（2）∵當斜率-A/B<0時
與證明有關
與證明有關又∵A>0
∴B>0
又∵原直線向上平移時,A和B為定值,因為B>0,又因為-C/B變大為-（C+△C)/B
∴經過分析得:△C<0
又∵Ax3+By3+C+△C=0
∴Ax3+By3+C>0
又∵原直線向下平移時,A和B為定值,因為B>0,又因為-C/B變小為-（C+△C)/B
∴經過分析得:△C>0
又∵Ax4+By4+C+△C=0
∴Ax4+By4+C<0
（3）∵由平移原直線可知上方可行域的〈所有計算點(x5,y5)〉令直線y>C，下方可行域的〈所有計算點(x6,y6)〉令直線y<C。
（4）∵由平移原直線可知左方可行域的〈所有計算點(x7,y7)〉令直線x<C，右方可行域的〈所有計算點(x8,y8)〉令直線x>C。
