線性獨立一般是指向量的線性獨立,指一組向量中任意一個向量都不能由其它幾個向量線性表示。
基本介紹
- 中文名:線性無關
- 外文名:linearly independent
- 所屬學科:數理科學
- 相關概念:線性表示、線性相關、線性相依等
概念引入

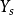
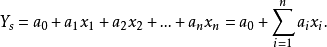
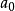
定義
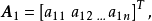
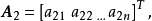

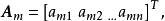

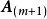



舉例說明

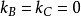

關係
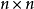

定理1

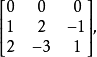
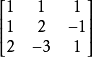
定理2


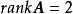


線性無關一般指本詞條
線性獨立一般是指向量的線性獨立,指一組向量中任意一個向量都不能由其它幾個向量線性表示。

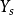
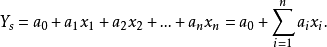
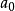
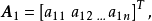
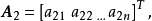

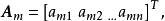

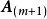




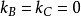

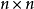


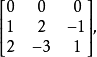
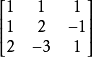


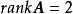


線上性代數裡,矢量空間的一組元素中,若沒有矢量可用有限個其他矢量的線性組合所表示,則稱為線性無關或線性獨立(linearly independent),反之稱為線性相關(linearly ...
設S是線性空間E的一個非空子集,如果S中任何有限個元都是線性無關的,則稱S為E的一個線性無關的集合。...
設有向量組A,如果在A中能選出r個向量a1,a2,...,ar,滿足(i)向量組A0:a1,a2,...,ar線性無關;(ii)向量組A中任意r+1個向量(如果A中有r+1個向量的...
最大線性無關組也稱為極大線性無關組,是代數中線性相關與線性無關中的基本概念。極大線性無關組表示一組向量中,由最多個線性無關的向量組成的部分,並且從這...
(3)線性代換把線性相關的向量組變成線性相關的向量組。注意:線性代換可能把線性無關的向量組變成線性相關的向量組[2] 。線性代換運算 編輯 ...
同時我們也可以看到,在三維空間中,變換矩陣表示為對角形的三個基向量是線性無關的,這個概念推廣就是我們一般的結論那就是一個nxn維變換矩陣能相識於一個對角形...
這兩個向量組可以互相線性表出,則稱這兩個向量組等價。注:(1)等價向量組具有傳逆性、對稱性、反身性;(2)向量組和它的極大線性無關組是等價向量組;(...
線性相關性(linear relatedness)複雜性測度間的一種特殊相關性.[1] 線性相關性(linear relatedness)複雜性測度間的一種特殊相關性.它是兩個複雜性測度在線性意義下...
線性分離性(linear disjointness of fields比域的代數無關更強的概念.設K, I.是域F的兩個擴域,它們都含於同一個擴域日之內.若K中任何一個在F上是線性無...
(這樣的同態稱為擴域間的F同態),若對K‘中某個元素組對每個xEK成立,則稱在K‘上是線性相關的;否則,稱為線性無關的.關於同態映射的相關性,戴德金(Dedekind,...
行滿秩矩陣就是行向量線性無關,列滿秩矩陣就是列向量線性無關;所以如果是方陣,行滿秩矩陣與列滿秩矩陣是等價的。中文名 滿秩矩陣 外文名 non-singular ...
反之,稱這組向量為線性無關的。更一般的,如果有無窮多個向量,我們稱這無窮多個向量是線性無關的,如果其中任意有限多個都是線性無關的。...
相關係數是最早由統計學家卡爾·皮爾遜設計的統計指標,是研究變數之間線性相關程度的量,一般用字母 r 表示。由於研究對象的不同,相關係數有多種定義方式,較為常用...
簡單相關係數又稱皮爾遜相關係數或“皮爾遜積矩相關係數”或叫線性相關係數,是指兩個定距變數間聯繫的緊密程度。相關係數可以看作是兩個隨機變數中得到的樣本集向量...
(6) 無相關(y不隨x增減呈線性關係),見圖6 [1] 。圖6 相關圖函式關係與相關關係 編輯 客觀現象之間總是相互聯繫和相互依存的,現象之間的數量依存關係有兩種...
