設S是線性空間E的一個非空子集,如果S中任何有限個元都是線性無關的,則稱S為E的一個線性無關的集合。
基本介紹
- 中文名:線性無關集
- 外文名:linearly independent set
- 適用範圍:數理科學
簡介
線性空間
線性無關

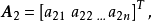





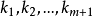

設S是線性空間E的一個非空子集,如果S中任何有限個元都是線性無關的,則稱S為E的一個線性無關的集合。

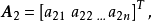





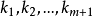

設S是線性空間E的一個非空子集,如果S中任何有限個元都是線性無關的,則稱S為E的一個線性無關的集合。...
線上性代數裡,矢量空間的一組元素中,若沒有矢量可用有限個其他矢量的線性組合所表示,則稱為線性無關或線性獨立(linearly independent),反之稱為線性相關(linearly ...
線性無閾是一種學說,是為了輻射防護的目的而做出的一種假設,是由高劑量照射得到的數據作線性外推而得到的,實際上偏高地估計了低劑量所產生輻射危害。...
設有向量組A,如果在A中能選出r個向量a1,a2,...,ar,滿足(i)向量組A0:a1,a2,...,ar線性無關;(ii)向量組A中任意r+1個向量(如果A中有r+1個向量的...
(3)線性代換把線性相關的向量組變成線性相關的向量組。注意:線性代換可能把線性無關的向量組變成線性相關的向量組。線性代換運算 編輯 ...
如上所述,一個向量空間的每一組基都是一個極大的線性無關集合,同時也是極小的生成集合。可以證明,如果向量空間擁有一組基,那么每個線性無關的子集都可以擴張成...
擬陣理論主要來自於對向量空間中線性無關的維度的深層次屬性的考量。對於這種方式定義的擬陣,有兩種表示方法:如果E是向量空間V的任意有限子集,通過將E中的線性無關...
[4] 對非零向量空間 V,基是 V 最小的生成集,也是極大線性無關組。如果一個向量空間 V 擁有一個元素個數有限的生成集,那么就稱 V 是一個有限維空間。向量...
齊次線性方程組的解集的極大線性無關組稱為該齊次線性方程組的基礎解系。基礎解系是線性無關的,簡單的理解就是能夠用它的線性組合表示出該方程組的任意一組解,...
