簡單相關係數又稱皮爾遜相關係數或“皮爾遜積矩相關係數”或叫線性相關係數,是指兩個定距變數間聯繫的緊密程度。相關係數可以看作是兩個隨機變數中得到的樣本集向量之間夾角的tan函式。
基本介紹
- 中文名:簡單相關係數
- 又名:皮爾遜相關係數
- 又稱:皮爾遜積矩相關係數
- 描述:兩個定距變數間聯繫的緊密程度
- 套用領域:數學
- 所屬科目:數學
簡介
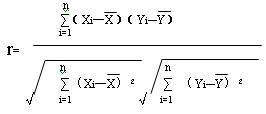


簡單相關係數又稱皮爾遜相關係數或“皮爾遜積矩相關係數”或叫線性相關係數,是指兩個定距變數間聯繫的緊密程度。相關係數可以看作是兩個隨機變數中得到的樣本集向量之間夾角的tan函式。
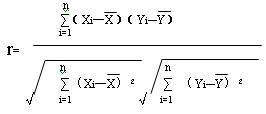


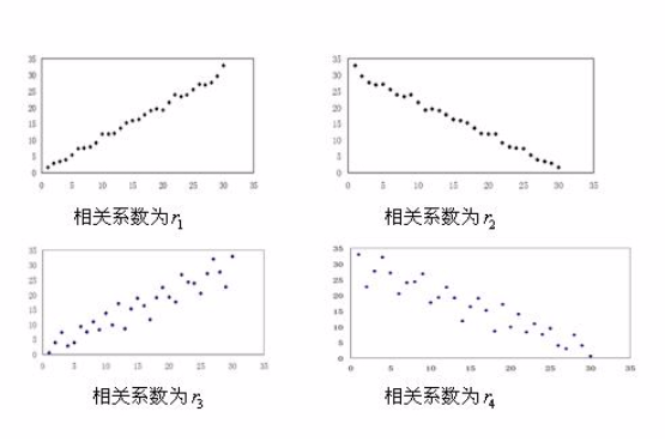
簡單相關係數又稱皮爾遜相關係數或“皮爾遜積矩相關係數”或叫線性相關係數,是指兩個定距變數間聯繫的緊密程度。相關係數可以看作是兩個隨機變數中得到的樣本集向量...
相關係數是最早由統計學家卡爾·皮爾遜設計的統計指標,是研究變數之間線性相關程度的量,一般用字母 r 表示。由於研究對象的不同,相關係數有多種定義方式,較為常用...
簡單相關是兩類變數之間線性或非線性的不確定的關聯關係,又稱二元相關、單相關。在簡單相關情形下,兩個變數之間相關關係,可能是正相關的或負相關的,或者是無相關...
在統計學中,皮爾遜積矩相關係數(Pearson product-moment correlation coefficient, PPMCC)用於度量兩個變數X和Y之間的相關(線性相關),其值介於-1與1之間。在自然...
皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是一種線性相關係數。皮爾森相關係數是用來反映...
Pearson相關係數(Pearson CorrelationCoefficient)是用來衡量兩個數據集合是否在一條線上面,它用來衡量定距變數間的線性關係。...
簡單相關分析是對兩個變數(一個自變數和因變數)間的相關關係的分析方法。相關關係是變數數值間的一種不確定的相互依存關係。在自然界和社會中,由於受各種因素的...
多重相關係數,亦稱復相關係數,指一個隨機變數與某一組隨機變數間線性相依性的度量。...
在統計學中,皮爾遜相關係數( Pearson correlation coefficient),又稱皮爾遜積矩相關係數(Pearson product-moment correlation coefficient,簡稱 PPMCC或PCCs),是用於度量...
復相關係數R0.12…n的測定,可先求出 x0對一組變數x1,x2,…,xn的回歸直線,再計算x0與用回歸直線估計值憫之間的簡單直線回歸。復相關係數為...
在 統計學中, 以查爾斯·斯皮爾曼命名的斯皮爾曼等級相關係數,即spearman相關係數。經常用希臘字母ρ表示。 它是衡量兩個變數的依賴性的 非參數 指標。 它利用...
相關性不等於因果性,也不是簡單的個性化,相關性所涵蓋的範圍和領域幾乎覆蓋了我們...相關性係數的計算過程可表示為:將每個變數都轉化為標準單位,乘積的平均數即為...
在統計學中,皮爾遜積矩相關係數(英語:Pearson product-moment correlation coefficient,又稱作 PPMCC或PCCs, 文章中常用r或Pearson's r表示)用於度量兩個變數X和Y...
判定係數(coefficient of determination),也叫可決係數或決定係數,是指線上性回歸中,回歸平方和與總離差平方和之比值,其數值等於相關係數的平方。它是對估計的回歸...
講述了根與係數的關係,分為偏相關係數,典型相關係數。具體為韋達定理。...... 根與係數的關係定律定義 編輯 根與係數的關係簡單相關係數: 又叫相關係數或線性相關...
若r是兩個變數之間的積矩相關係數,則疏遠係數等於線性回歸中非判定係數的平方根。這一詞通常用於心理學、生物科學等領域,由T. L. Kelley於1919年提出。...
