基本介紹
- 中文名:皮爾遜相關係數
- 外文名:Pearson correlation coefficient
- 簡單別名:簡單相關係數
- 別名:皮爾遜積矩相關係數
- 定義者:皮爾遜
定義
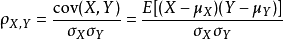
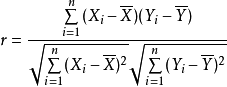
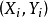
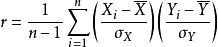
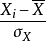
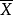
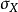
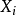
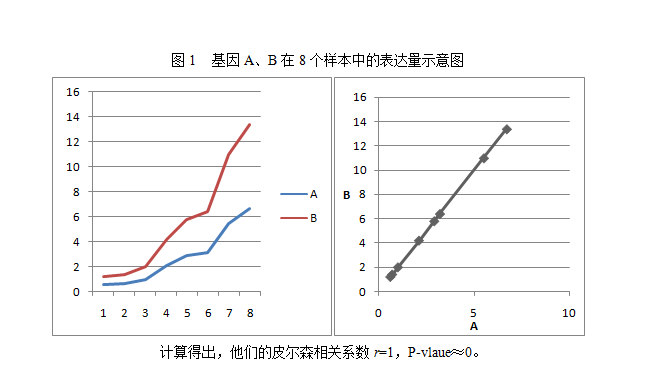
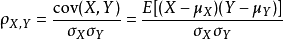
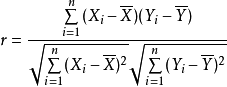
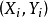
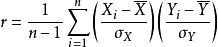
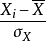
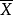
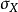
皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是一種線性相關係數。皮爾森相關係數是用來反映...
Pearson相關係數(Pearson CorrelationCoefficient)是用來衡量兩個數據集合是否在一條線上面,它用來衡量定距變數間的線性關係。...
簡單相關係數又稱皮爾遜相關係數或“皮爾遜積矩相關係數”或叫線性相關係數,是指兩個定距變數間聯繫的緊密程度。相關係數可以看作是兩個隨機變數中得到的樣本集向量...
在統計學中,皮爾遜相關係數( Pearson correlation coefficient),又稱皮爾遜積矩相關係數(Pearson product-moment correlation coefficient,簡稱 PPMCC或PCCs),是用於度量...
在統計學中,皮爾遜積矩相關係數(英語:Pearson product-moment correlation coefficient,又稱作 PPMCC或PCCs, 文章中常用r或Pearson's r表示)用於度量兩個變數X和Y...
皮爾遜相關係數,是用來度量兩個變數 X 和 Y 之間的相互關係(線性相關)的,取值範圍在 [-1,+1] 之間。...
Microsoft Excel 中 PEARSON函式,返回 Pearson(皮爾生)乘積矩相關係數 r,這是一個範圍在 -1.0 到 1.0 之間(包括 -1.0 和 1.0 在內)的無量綱指數,反映...
同配係數(Assortativity coefficient)是一種基於“度”的皮爾森相關係數,用來度量相連節點對的關係。結果r為正值代表具有相同度的點之間有某種協同關係,負值表示具有不...
2.2.2 皮爾森相關係數 15 2.3 推斷統計 16 2.3.1 參數估計 16 2.3.2 假設檢驗 20 2.3.3 假設檢驗的阿里雲實現 23 小結28 習題28 第3章 關聯分析...
這一步就是尋找與你距離最近的用戶,測算距離一般採用以下三種算法: 1.皮爾森相關係數。 2.餘弦相似性。 3調整餘弦相似性。 調整餘弦 相似性似乎效果會好一些。...
並分別以中國消費者和西方消費者為研究對象,主要運用了皮爾森相關係數檢驗、兩獨立樣本非參數檢驗、多個獨立樣本的K-W檢驗、判別分析等數學分析方法,考察了模型中各...
31.9.2 皮爾森相關係數r 493 31.9.3 多變數描述統計中的NULL值 493 31.10 SQL:2006中的統計函式 494 31.10.1 方差、標準偏差以及描述統計 494 31.10.2...
