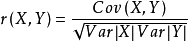樣本相關係數

在統計學中，皮爾遜積矩相關係數（Pearson product-moment correlation coefficient， PPMCC）用於度量兩個變數X和Y之間的相關（線性相關），其值介於-1與1之間。在自然科學領域中，該係數廣泛用於度量兩個變數之間的相關程度。樣本相關係數是指樣本中變數之間的線性相關程度。

基本介紹

• 中文名：樣本相關係數
• 外文名：Sample Correlation coefficient
• 學科：計算機、統計學
• 定義：樣本中變數之間的線性相關程度
• 有關術語：相關係數
• 領域：數據分析

簡介

樣本是藉助於特殊方法抽出而組成總體的一部分。樣本的主要特點是： 它代表總體；它的容量小於總體容量。樣本相關係數是指樣本中變數之間的線性相關程度。樣本相關係數準確性與很多因素都有關，如抽樣方法，樣本的容量。樣本相關係數的計算公式如下：

其中Cov(X,Y)為X與Y的協方差，Var[X]為X的方差，Var[Y]為Y的方差。r的取值範圍為-1≤r≤1，當r接近±1時表明觀察的數據線性相關較強，當r接近0時表明觀察數據無線性相關。當用樣本相關係數來反映總體的變數之間是否相關，在樣本容量比較小時通常需要進行相關係數的檢驗。

抽樣方法

在統計學中，抽樣（Sampling）是一種推論統計方法，它是指從目標總體（Population，）中抽取一部分個體作為樣本（Sample），通過觀察樣本的某一或某些屬性，依據所獲得的數據對總體的數量特徵得出具有一定可靠性的估計判斷，從而達到對總體的認識。

簡單隨機抽樣（simple random sampling），也叫純隨機抽樣。從總體N個單位中隨機地抽取n個單位作為樣本，使得每一個容量為樣本都有相同的機率被抽中。特點是：每個樣本單位被抽中的機率相等，樣本的每個單位完全獨立，彼此間無一定的關聯性和排斥性。簡單隨機抽樣是其它各種抽樣形式的基礎。通常只是在總體單位之間差異程度較小和數目較少時，才採用這種方法[1]。

系統抽樣（systematic sampling），也稱等距抽樣。將總體中的所有單位按一定順序排列，在規定的範圍內隨機地抽取一個單位作為初始單位，然後按事先規定好的規則確定其他樣本單位。先從數字1到k之間隨機抽取一個數字r作為初始單位，以後依次取r+k、r+2k……等單位。這種方法操作簡便，可提高估計的精度。

分層抽樣（stratified sampling）。將抽樣單位按某種特徵或某種規則劃分為不同的層，然後從不同的層中獨立、隨機地抽取樣本。從而保證樣本的結構與總體的結構比較相近，從而提高估計的精度。

整群抽樣（cluster sampling）。將總體中若干個單位合併為組，抽樣時直接抽取群，然後對中選群中的所有單位全部實施調查。抽樣時只需群的抽樣框，可簡化工作量，缺點是估計的精度較差。

相關係數

相關關係是一種非確定性的關係，相關係數是研究變數之間線性相關程度的量。由於研究對象的不同，相關係數有如下幾種定義方式。

簡單相關係數：又叫相關係數或線性相關係數，一般用字母P 表示，是用來度量變數間的線性關係的量。

復相關係數：又叫多重相關係數。復相關是指因變數與多個自變數之間的相關關係。例如，某種商品的季節性需求量與其價格水平、職工收入水平等現象之間呈現復相關關係。

典型相關係數：是先對原來各組變數進行主成分分析，得到新的線性關係的綜合指標，再通過綜合指標之間的線性相關係數來研究原各組變數間相關關係。

數據分布的敏感度

存在性

總體皮爾遜相關係數被定義成矩，因此任意的雙變數機率分布是非零的，也就是說總體協方差和邊緣總體方差是由定義的。一些機率分布，諸如柯西分布有未定義的方差，因此X or Y 如果服從這種分布，ρ便是未定義的。在實際套用中，如果有數據被懷疑服從重尾分布，這個條件就需要引起重視。然而，相關係數的存在性通常並需要太介意；例如，如果分布是有界的，ρ便總是有意義的。

大樣本的特性

在雙變數常態分配的案例中，只要邊緣均值和方差是已知的，總體相關係數描述的是便是聯合分布。在其他的雙變數分布中，這個結論並不正確。總之，不論兩個隨機變數的聯合分布是不是正態的，相關係數在研究的它們之間的線性依賴性都是有幫助的。樣本相關係數是對兩個常態分配變數總體相關係數的最大似然估計並且是漸進無偏的和有效的，這也就是說如果數據是正態的並且樣本容量是中等的或大量的，就不可能構造出一個比樣本相關係數更準確的估計。對於非正態的數據，樣本相關係數大致上是無偏的，但有可能是無效的。只要樣本均值、方差和協方差是一致的（當大數定理可以套用的情況下），樣本相關係數是總體相關係數的 一致估計 。

穩健性

與其他常用的統計指標相似的，樣本指標r不是穩健的。因此如果由異常值，這個指標是有誤導性的。特別的，PMCC 既不是穩健分布的，也不是異常值穩健的)。對X 和 Y的散點圖的觀察可以很明顯的揭示出缺乏穩健性的情況，在這種情況下，採用的聯合的方法是比較明智的。注意到，雖然大多數穩健的估計器從某種程度上說都是有統計依賴的，它們總的來說，在總體相關係數的尺度上都是可辨的。

基於皮爾遜相關係數的統計推斷對數據分散式敏感的。 如果數據大致是常態分配的，可以使用精確檢驗和基於Fisher變換的漸進檢驗，但是它們可能由誤導性。 在一些情況下，自助採樣可以用來構造置信區間。 同時， 重複抽樣 可以套用在假設檢驗中。 這些非參數化 的方法在某些情況下，如雙變數常態分配不能保證時，可能得出更有意義的結論。然而，這些方法的標準形式依賴於數據的 可交換性。這也就意味著被分析的數據時沒有順序的和組別的。因為這有可能會影響估計相關係數的特性。

分層分析是一種容許缺少雙變數正態性的方法，或者說是用來隔離相互關聯因素的關聯結果。 如果W代表聚類成員或者其它需要被控制的因素，我們可以分離基於W的數據, 然後我們可以再每個層里計算相關係數。 當我們控制變數W，我們便能在層的等級上估計與所有相關係數相關的各自的相關係數。