基本介紹
- 中文名:spearman相關係數
- 外文名:Spearman's rank correlation coefficient
- 定義:衡量分級定序變數之間的相關程度
- 用途:描述數據間的相關性
定義和計算
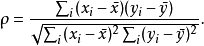
| 變數Xi | 降序位置 | 等級xi |
|---|---|---|
0.8 | 5 | 5 |
1.2 | 4 | |
1.2 | 3 | |
2.3 | 2 | 2 |
18 | 1 | 1 |
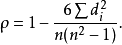
相關度量
解釋
顯著性的確定
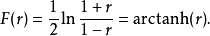
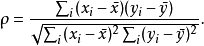
| 變數Xi | 降序位置 | 等級xi |
|---|---|---|
0.8 | 5 | 5 |
1.2 | 4 | |
1.2 | 3 | |
2.3 | 2 | 2 |
18 | 1 | 1 |
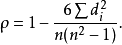
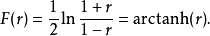
在 統計學中, 以查爾斯·斯皮爾曼命名的斯皮爾曼等級相關係數,即spearman相關係數。經常用希臘字母ρ表示。 它是衡量兩個變數的依賴性的 非參數 指標。 它利用...
Pearson相關係數 [1] (Pearson CorrelationCoefficient)是用來衡量兩個數據集合是否在一條線上面,它用來衡量定距變數間的線性關係。中文名 Pearson相關係數 外文名 ...
皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是一種線性相關係數。皮爾森相關係數是用來反映...
秩相關係數,亦稱為“等級相關係數”,是反映等級相關程度的統計分析指標。常用的等級相關分析方法有Spearman相關係數和 [1] 等。如果秩相關係數為正,則 隨著 的增加...
等級相關係數亦稱為“秩相關係數”,是反映等級相關程度的統計分析指標,常用的等級相關分析方法有Spearman等級相關和Kendall等級相關等。...
斯皮爾曼等級相關(Spearman’s correlation coefficient for ranked data)主要用於解決稱名數據和順序數據相關的問題。適用於兩列變數,而且具有等級變數性質具有線性...
Gamma相關係數:衡量兩個次序尺度變數之相關性。Spearman等級相關係數:衡量兩個次序尺度變數之相關性。Kendall等級相關係數(Kendall tau rank correlation coefficient):...
在統計學中,皮爾遜相關係數(Pearson correlation coefficient),通常用 R 或ρ 表示,是用來度量兩個變數 X 和 Y 之間的相互關係(線性相關)的,取值範圍在 [-1,+...
Microsoft Excel 中 PEARSON函式,返回 Pearson(皮爾生)乘積矩相關係數 r,這是一個範圍在 -1.0 到 1.0 之間(包括 -1.0 和 1.0 在內)的無量綱指數,反映...
雖然Fisher變換主要與雙變數正態觀測的Pearson積矩相關係數有關,但在更一般的情況下,它也可以套用於Spearman秩相關係數。類似結果對於漸近分布適用,但需要較小的調整...
12.7.1 Pearson相關係數的檢驗 12.7.2 Spearman秩相關檢驗 12.7.3 Kendall τ相關檢驗 12.7.4 多變數Kendall協和係數檢驗 12.8 一致性檢驗 12.8....
9.5.3肯氏相關係數τ?b結果分析9.6斯皮爾曼等級相關9.6.1斯皮爾曼等級相關係數的計算公式9.6.2用“分析家”對話框測量等級相關9.6.3Spearman相關係數的...
