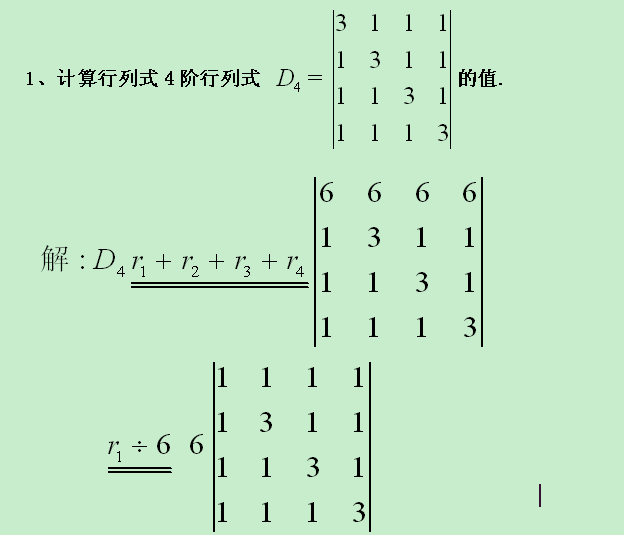
基本介紹
- 中文名:行列式
- 外文名:determinant(英文)déterminant(法文)
- 表達式:D=|A|=detA=det(aij)
- 套用學科:線性代數
- 適用領域範圍:數學、物理學
- 分類:二階行列式,三階行列式
數學定義
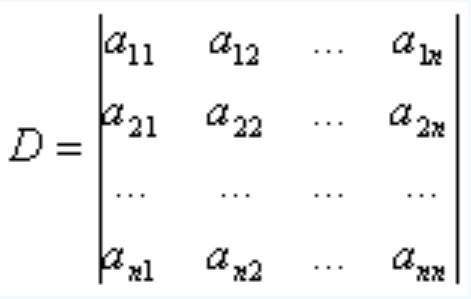


若n階方陣A=(aij),則A相應的行列式D記作
D=|A|=detA=det(aij)
若矩陣A相應的行列式D=0,稱A為奇異矩陣,否則稱為非奇異矩陣.
標號集:序列1,2,...,n中任取k個元素i1,i2,...,ik滿足
1≤i1<i2<...<ik≤n(1)
i1,i2,...,ik構成{1,2,...,n}的一個具有k個元素的子列,{1,2,...,n}的具有k個元素的滿足(1)的子列的全體記作C(n,k),顯然C(n,k)共有

σ={i1,i2,...,ik}
是{1,2,...,n}的滿足(1)的一個子列.若令τ={j1,j2,...,jk}∈C(n,k),則σ=τ表示i1=j1,i2=j2,...,ik=jk。