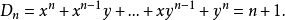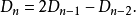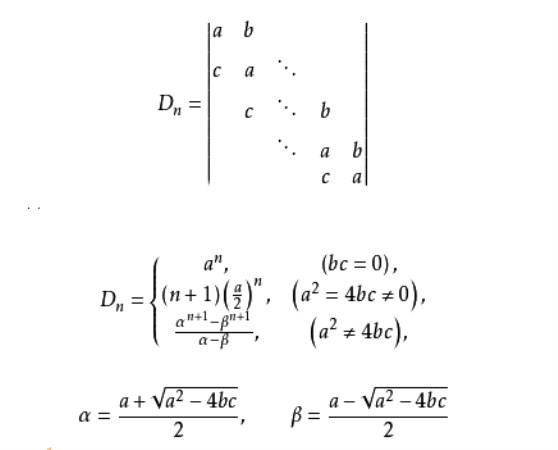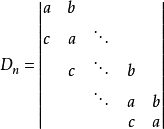帶形行列式

帶形行列式是一種特殊形狀的行列式，形如帶狀的n階行列式稱為帶形行列式，其中主對角線上的元素全是a，與主對角線平行的兩條線上的元素分別全為b和c，其餘的元素全是零。

基本介紹

• 中文名：帶形行列式
• 外文名：Belt  determinant
• 所屬學科：數學
• 所屬問題：高等代數（行列式）
• 簡介：形如帶狀的n階行列式

基本介紹

帶形行列式即形如

的n階行列式稱為帶形行列式，其中主對角線上的元素全是a，與主對角線平行的兩條線上的元素分別全為b和c，其餘的元素全是零。帶形行列式

式中

是二次方程x²-ax+bc=0的根。

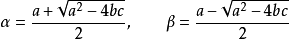
例題解析

以下例題的行列式都是帶形行列式。

【例1】計算下列行列式：

分析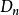 主對角線上元素全是x +y，與其平行的上方元素全是xy,而下方元素全是1.因此可試探利用拆項法或先從D₂，D₃尋求規律再用數學歸納法證明的方法。

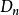
解法1拆項法。

按第一列把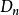 拆成兩個行列式相加，然後對第一個行列式從第一列開始，每列都乘-y往下一列加，得

再將 按另一種方法拆項，類似可得

由(1)x-(2)y，得

當x≠y時得

當x=y時，由(1)並進一步可得

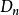
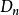
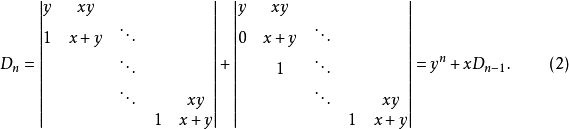
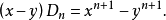
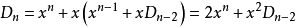
即(3)式也是對的。

解法2 用數學歸納法證明。

即先計算特殊的 ，從中得出結論再用數學歸納法證明一般結論的方法，此法往往是有效的。

由直接驗算易知:

於是推測 (4)

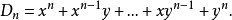
假設當n<k時(4)式成立，下證n=k時(4)式成立。

對D_k按第一行展開，得

但由歸納假設，將 代人上式， 得

即(4)式對n=k也成立，得證。

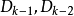
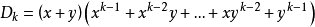
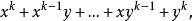
【例2】計算下列行列式：

解 ：在上題中取x=y=1即得

另證法如下：對D_n按第一行(或列)展開，得遞推公式

由此得 據此又得