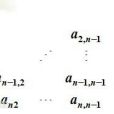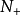斜下三角行列式

斜下三角行列式和斜上三角行列式的數值一樣，

為(-1)^(n(n-1))/2 a1n a2,n-1...an-1,2 an1

基本介紹

• 外文名：Oblique triangular determinant
• 別稱：次下三角行列式
• 套用學科：線性代數
• 適用領域範圍：行列式

定律定義

對於n階的斜下三角行列式下列公式。

特別地，斜對角行列式

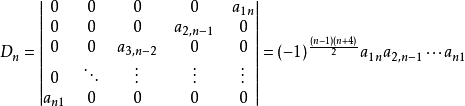
推導過程

降階法

按定義將第一行反覆展開。

（n-1階）

（n-2階）

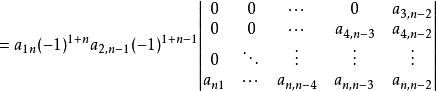
由於乘上（-1）^-2n+2=1不改變上式的符號，亦可寫作 。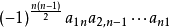

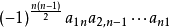
數學歸納法

猜想：

成立。當n=1時，D₁=|a_1n|=(-1)⁰a_1n=a_1n,成立。

假設n=k-1（k且k>1）等式也成立。由假設,少一階的行列式：

當n=k時，按行列式定義展開第一行，D_k=（-1）a_1kM_1K。

從而，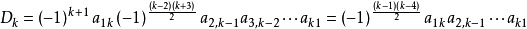

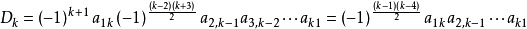
有數學歸納法得，猜想成立，證畢。