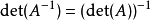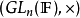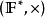行列式在數學中，是由解線性方程組產生的一種算式。行列式的特性可以被概括為一個多次交替線性形式，這個本質使得行列式在歐幾里德空間中可以成為描述“體積”的函式。
其定義域為nxn的矩陣A，取值為一個標量，寫作det(A)或 | A | 。行列式可以看作是有向面積或體積的概念在一般的歐幾里得空間中的推廣。或者說，在n維歐幾里得空間中，行列式描述的是一個線性變換對“體積”所造成的影響。無論是在線性代數、多項式理論，還是在微積分學中（比如說換元積分法中），行列式作為基本的數學工具，都有著重要的套用。 行列式概念最早出現在解線性方程組的過程中。十七世紀晚期，關孝和與萊布尼茨的著作中已經使用行列式來確定線性方程組解的個數以及形式。十八世紀開始，行列式開始作為獨立的數學概念被研究。
十九世紀以後，行列式理論進一步得到發展和完善。矩陣概念的引入使得更多有關行列式的性質被發現，行列式在許多領域都逐漸顯現出重要的意義和作用，出現了線性自同態和向量組的行列式的定義[1] 。
續文,基本性質,行列式的展開,余因式,代數餘子式,行列式關於行和列的展開,計算,函式,單變數的行列式函式,矩陣的行列式函式,
續文
因中文百科詞條公式數量限制，行列式詞條內容剩餘部分展示在此詞條中。
基本性質
行列式的一些基本性質，可以由它的多線性以及交替性推出。
- 在行列式中，一行（列）元素全為0，則此行列式的值為0。
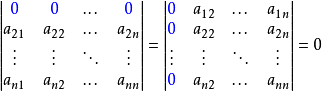
- 在行列式中，某一行（列）有公因子k，則可以提出k。
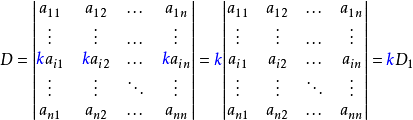
- 在行列式中，某一行（列）的每個元素是兩數之和，則此行列式可拆分為兩個相加的行列式。
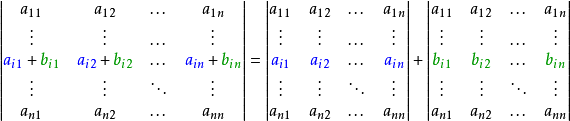
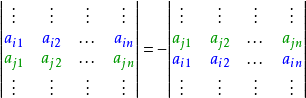
- 行列式中的兩行（列）互換，改變行列式正負符號。
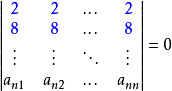
- 在行列式中，有兩行（列）對應成比例或相同，則此行列式的值為0。
- 將一行（列）的k倍加進另一行（列）里，行列式的值不變。
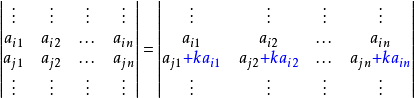
- 注意：一行（列）的k倍加上另一行（列），行列式的值改變。
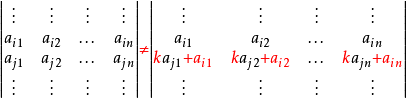
- 將行列式的行列互換，行列式的值不變，其中行列互換相當於轉置。這個性質可以簡單地記作
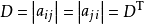
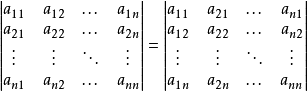
- 行列式的乘法定理：方塊矩陣的乘積的行列式等於行列式的乘積。
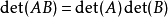
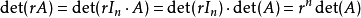
·以上的乘法公式還可以進一步推廣為所謂柯西–比內公式，從而使得只要兩個矩陣的乘積是方塊矩陣，就有類似於以上的結果：假設A是一個矩陣，而B是一個矩陣。如果S是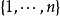
中具有m個元素的子集
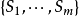，我們記AS為A中列指標位於S中的子矩陣。類似地，記BS為B中行指標位於S中的子矩陣。那么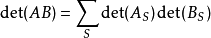
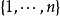
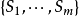
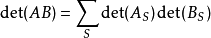
這裡求遍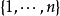
中m個元素的所有可能子集S（共有C(n,m)個）。
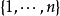
如果m=n，即A與B是同樣大小的方塊矩陣，則只有一個容許集合S，柯西–比內公式退化為通常行列式的乘法公式。如過m= 1則有n容許集合S，這個公式退化為點積。如果m>n，沒有容許集合S，約定行列式det(AB)是零。
·若A是可逆矩陣，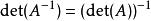
。
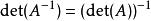
·若將方塊矩陣中的元素取共軛，得到的是矩陣的共軛矩陣。共軛矩陣的行列式值等於矩陣行列式值的共軛：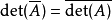
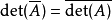
·若兩個矩陣相似，那么它們的行列式相同。這是因為兩個相似的矩陣之間只相差一個基底變換，而行列式描述的是矩陣對應的線性映射對體積的影響，而不是體積，所以基底變換並不會影響行列式的值。用數學語言來說，就是：
如果兩個矩陣A與B相似，那么存在可逆矩陣P使得，所以
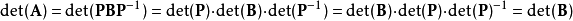
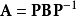
·由於三角矩陣的行列式計算簡便，當矩陣的係數為域時，可以通過高斯消去法將矩陣變換成三角矩陣，或者將矩陣分解成三角矩陣的乘積之後再利用行列式的乘法定理進行計算。可以證明，所有的矩陣A都可以分解成一個上三角矩陣U、一個下三角矩陣L以及一個置換矩陣P的乘積：
。這時，矩陣A的行列式可以寫成：
·分塊矩陣的行列式並不能簡單地表示成每個分塊的行列式的乘積組合。對於分塊的三角矩陣，仍然有類似的結論：
，矩陣的行列式等於對角元素的行列式之乘積。
對於一般情況，若對角元素中有一個是可逆矩陣，比如說A可逆，那么矩陣的行列式可以寫做
行列式的展開
余因式
又稱“餘子式”、“余因子”。參見主條目余因式。
對一個n階的行列式M，去掉M的第i行第j列後形成的n-1階的行列式叫做M關於元素mij的余因式。記作
。
代數餘子式
M關於元素mij的代數餘子式記作
。
行列式關於行和列的展開
一個n階的行列式M可以寫成一行（或一列）的元素與對應的代數餘子式的乘積之和，叫作行列式按一行（或一列）的展開。
這個公式又稱拉普拉斯公式，把n維矩陣的行列式計算變為了n個n-1維的行列式的計算。另一方面，拉普拉斯公式可以作為行列式的一種歸納定義：在定義了二維行列式後，n維矩陣的行列式可以藉助拉普拉斯公式用n-1維的行列式來定義。這樣定義的行列式與前面的定義是等價的。
計算
計算行列式的值是一個常見的問題。最簡單的方法是按照定義
計算或按照拉普拉斯公式進行遞歸運算。這樣的算法需要計算
次的加法，複雜度是指數函式。在實際的計算中只能用於計算階數很小的行列式。注意到拉普拉斯公式的性質，如果一行或一列裡面有很多個0，那么就可以把行列式按這一行或一列展開，這時數值為零的係數所對應的代數餘子式就不必計算了，因為最後要乘以0，這樣就可以簡化計算。然而更加簡便的算法是利用高斯消去法或LU分解法，把矩陣通過初等變換變成三角矩陣或三角矩陣的乘積來計算行列式的值。這些算法的複雜度都是n3級別，遠遠小於直接計算的複雜度。
如果一個算法可以在
時間內算出矩陣乘法，那么可以構造出一種
時間內的行列式求值算法。這說明求矩陣的行列式的值和矩陣的乘法有相同的複雜度。於是，通過分治算法或者其它的方法，可以達到比
更好的結果。比如，存在複雜度
的行列式求值算法。
函式
由行列式的一般表達形式中可以看出，矩陣A的行列式是關於其元素的多項式。因此行列式函式具有良好的光滑性質。
單變數的行列式函式
設矩陣函式
為
（k階連續可導）的函式，則由於行列式函式
只不過是矩陣
的某些係數的乘積，所以也是
的。其對t的導數為
，其中的每個
是矩陣
的第i個行向量（也可以全部是列向量）。
