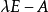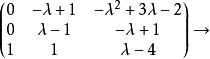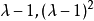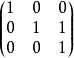若爾當標準型是由若干個主對角線為特徵值，下方（或上方）次對角線全為1，其餘全為0的若爾當塊按對角排列組成的準對角矩陣。不是每個n階矩陣通過初等變換都能化為對角矩陣，但每個n階複數矩陣A通過初等變換都能化為若爾當標準型，這個若爾當形矩陣除去其中若爾當塊的排列次序不同外是被矩陣A唯一確定的，它稱為矩陣A的若爾當標準型。
基本介紹
- 中文名：若爾當標準型
- 外文名：Jordan standard form
- 套用學科：線性代數
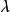
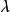
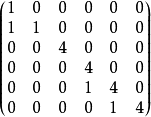
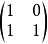
定義,若爾當塊,若爾當標準型,實例,若爾當塊實例,若爾當標準型實例,理論推導與例子,
定義
若爾當塊
形式為
的矩陣稱為若爾當塊（其中
為複數）。即若當塊矩陣對角線上為相同的複數，下方（或上方）次對角線上全為1，其餘元素全為0。
若爾當標準型
由若干個若爾當塊組成的準對角矩陣稱為若爾當標準型，其一般形狀為
，其中
，並且
中有一些可以相等。
實例
若爾當塊實例
例如
，
，
都是若爾當塊。
若爾當標準型實例
例如
是一個若爾當標準型矩陣。其由
，
，
等三個若爾當塊組成。
理論推導與例子
一般採用初等因子理論來完成若爾當標準型的理論推導，其具體推導過程參見王萼芳《高等代數》346-349頁。這裡我們採用一個具體的例子來說明若爾當標準型的計算過程。
例：求矩陣
的若爾當標準型。
解：首先求
的初等因子：
因此，A的初等因子是
，A的若爾當標準型是
