基本介紹
- 中文名：例外若爾當代數
- 外文名：exceptional Jordan algebra
- 領域：代數
- 對應概念：特殊若爾當代數
- 本質：若爾當代數
- 提出者：若爾當
概念介紹,若爾當代數,特殊若爾當代數,特殊若爾當代數實例,Hermitian 若爾當代數,衍生和結構代數,人物簡介,
概念介紹
例外若爾當代數(exceptional Jordan algebra)與特殊若爾當代數相對照的一種若爾當代數。一個若爾當代數不是特殊的若爾當代數即稱為例外若爾當代數。著名的例外若爾當代數的例子是在一個凱萊一迪克森代數C上定義一個對合，然後考慮C上某些3階方陣所構成的一個集合H(C)，使得H(C)是若爾當代數，但它不是任何特殊若爾當代數的同態像。
若爾當代數
若爾當代數(Jordan algebra)是20世紀30年代初由物理學家若爾當((Jordan,P.)引出來的，最初的目的是推廣量子力學的公式。他們最初被稱為“r階數字系統”，但由Albert（1946年）更名為“若爾當代數”，他開始系統研究若爾當代數。
在抽象代數中，若爾當代數是一個不相關代數，其乘法滿足以下公理： xy = yx; (xy)(xx)= x(y(xx))。
若爾當代數中的兩個元素x和y的乘積也表示為x∘y，為了避免與相關關聯代數的乘積混淆。
若爾當代數(Jordan algebra)是一種交換的非結合代數。它滿足若爾當恆等式。所謂非結合代數滿足若爾當恆等式，是指對它的任意元素x，y，恆有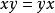
及
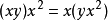。任何交換(結合)代數都是若爾當代數。特徵數為0的域F上的任意有限維半單的若爾當代數恆可惟一地表為其單理想之直和。對於有限維若爾當代數，理想是可解的、冪零的和詣零的三條件等價。若爾當代數是20世紀30年代初由物理學家若爾當((Jordan,P.)引出來的，最初的目的是推廣量子力學的公式。
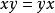
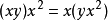
特殊若爾當代數
x°y=(xy+yx)/2 (任意x，y∈B)，
則(B，+，°)是F上的一個若爾當代數，通常記為B+。域F上的非結合代數A，若同構於某個B+的子代數，則稱A為特殊若爾當代數。
特殊若爾當代數實例
給定一個關聯代數A，可以使用相同的底層加法向量空間來構造若爾當代數
。請注意，若且唯若是交換代數時，關聯代數才是若爾當代數。如果不可交換，我們可以在A上定義一個新的乘法，使其交換，實際上使它成為Jordan代數。新的乘法x∘y滿足：
Hermitian 若爾當代數
如果（A，σ）是具有回歸σ的關聯代數，則如果σ（x）= x和σ（y）= y，則遵循：
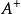
示例
1.一組自相關實數，複數或四元數矩陣滿足如下乘法：
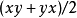
2.一組3×3自相關矩陣在八次數上，同樣滿足乘法：
衍生和結構代數
約旦代數A的衍生形式是A的同態D，使得D（xy）= D（x）y + xD（y）。導數形成李代數der(A)。約旦身份意味著如果x和y是A的元素，那么將z代入到x(yz)-y(xz)的同態是推導。因此，A和der（A）的直接和可以形成一個稱為A，str（A）的結構代數的李代數。
一個簡單的例子由Hermitian Jordan代數H（A，σ）提供。在這種情況下，具有σ（x）= - x的A的任何元素x定義了導數。在許多重要的例子中，H（A，σ）的結構代數為A。
人物簡介
若爾當是法國數學家。生於里昂，卒於巴黎。畢業於巴黎理工科大學，1861年獲博士學位。1873—1921年任教於母校和法蘭西學院，1881年當選為法國科學院院士。1895年當選為彼得堡科學院通訊院士。擔任過《純粹與套用數學》雜誌編輯(1885—1921)。若爾當在代數學、分析學、函式論、拓撲學、集合論等方面都有較大的貢獻。他運用組合論的觀點探討了多面體的對稱性，對平面或n維空間的任意集合引入了外測度的概念;還建立了有界變差函式的概念，並證明這種函式可表為兩個增函式的差;在代數學方面，他系統地發展了有限群論及伽羅華理論，證明了著名的“若爾當—赫爾德定理”的前半部。他最早開展了無限群的研究，首先用形如：
