基本介紹
- 中文名:非結合代數
- 外文名:Non associative algebra
- 領域:代數
- 對應概念:結合代數
- 實例:李代數、若爾當代數
- 推廣:非交換若爾當代數、右交錯代數
定義
環論
類型
李代數
若爾當代數

交錯代數
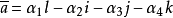


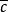

冪結合代數
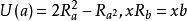
理論發展
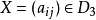
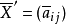

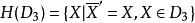


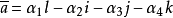


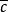

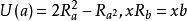
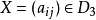
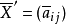

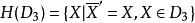

非結合代數,non-associative algebra,一般環論中的一個分支,與結合代數在方法和內容上都有非常密切的聯繫。環論是研究具有兩種結合法的特殊代數系——環的科學。代...
結合代數(associative algebra):一種代數系統,類似於群、環、域,而更接近於環。結合代數的研究,早在19世紀50年代,W.R.哈密頓考察四元數、H.G.格拉斯曼引入向量...
定義 自由非結合代數(free nonassociative algebra)一種具有泛性的非結合代數.域F上的一個非結合代數稱為是F上由xi,xZ,...,x,生成的有1的自由非結合代數,記...
定義 冪零非結合代數(nilpotent nonassociative algebra)一類特殊的非結合代數.設A是域F上的一個非結合代數,若有正整數n,使得A中任意n個元素以任何順序相乘之積...
結合代數的定義中把乘法結合律刪去,就是非結合代數。 嘉當子代數(Cartan subalgebra)是研究李代數分解時常用的一類子代數。設L為域F上的李代數,若L的子代數h...
在抽象代數中,交錯代數是乘法不滿足結合性,僅滿足交錯性的代數。也就是說,我們有:x(xy) = (xx)y (yx)x = y(xx) 對於所有代數中的x和y。每一個結合...
卡茨一穆迪代數(Kac-Moody algebra)李代數的一個新分支。是卡茨(Kac, V.)和穆迪(Moody, R.)分別於1967,1968年獨立引入的。李代數是一類重要的非結合代數。非...
若爾當代數(Jordan algebra)是一種交換的非結合代數。它滿足若爾當恆等式。所謂非結合代數滿足若爾當恆等式,是指對它的任意元素x,y,恆有 及 。任何交換(結合)...
結合子(associator)是在非結合代數中用來度量給定的三個元素結合性的一個元素。設A是非結合代數,對任意x,y,z∈A,稱(x,y,z)=(xy)z-x(yz)為x,y,z的...
對稱代數左對稱代數 編輯 左對稱代數(或Vinberg代數,Koszul代數,擬結合代數等)是一類重要的非結合代數。它在數學和數學物理中起重要作用。它的研究可以直接促進其它...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了. 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了,到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量代數...
定義 嚴格冪結合代數(strictly power associative algebra)一種特殊的冪結合代數.若A是域F上的一個非結合代數,且對F的每個擴張K,其純量擴張A} -A⑧ FK都是K...
若爾當代數(Jordan algebra)是一種交換的非結合代數。它滿足若爾當恆等式。所謂非結合代數滿足若爾當恆等式,是指對它的任意元素x,y,恆有 及 。任何交換(結合)...
可解代數(solvable algebra)是一類非結合代數。...... 設A是域F上的一個非結合代數,若有正整數n使得在其導出列中Acn> - 0,則稱A是個可解代數.非結合代數A...
《抽象代數Ⅱ——結合代數》是一部出版的圖書,作者是王立雲。...... 而成,內容包括結合代數,張量積、張量代數,二次型、Clifford代數,群代數及其表示,某些非結合...
李代數(Lie algebra)是一類重要的非結合代數。最初是由19世紀挪威數學家索菲斯·李創立李群時引進的一個數學概念,經過一個世紀,特別是19世紀末和20世紀的前葉,...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了. 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展.與外代數,對稱代數,張量...
特殊若爾當代數(special Jordan algebra)是一種特殊類型的若爾當代數。它與某個結合代數有關係。若爾當代數(Jordan algebra)是20世紀30年代初由物理學家若爾當((...
導子代數(derivation algebra)是指由給定的非結合代數派生的一個李代數。給定的非結合代數的一些線性變換做成的代數。非結合代數是抽象代數學的一個重要分支,與結合...
代數獨立是指在抽象代數里,一個域L的子集S若被稱做代數獨立於一子域K的話,表示S內的元素都不符合係數包含在K內的非平凡多項式。這表示任何以S內元素排成的...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了。到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量...
定義 二次型代數(quadratic algebra)一種特殊的非結合代數.設A是域F上的一個有1的非結合代數,若A的每個元素x都滿足一個如下形式的等式 其中t(x) ,n(x) ...
合成代數(composition algebra)是一類特殊的代數,它是一對對偶空間的張量積所成的代數。合成代數(A,*,N)是分數代數或分裂代數,取決於A中存在非零v,使得N(v)= ...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了. 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量...
第19節 Lie代數和非結合代數 A.Lie代數 Poisson括弧作為Lie代數的例子.Lie環和Lie代數. B.Lie理論 Lie群的Lie代數. C.Lie代數的套用 Lie群與剛體運動...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了。 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量...
在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了。 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。與外代數,對稱代數,張量...
