基本介紹
- 中文名:代數群
- 外文名:Algebraic group
- 領域:代數幾何
- 別名:群簇
- 範疇論中:代數簇範疇中的群對象
- 本質:群
預備知識
群
代數幾何
代數群的概念
代數群的性質

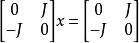



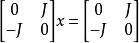


在代數幾何中,一個代數群(或群簇)是一個為代數簇的群,其簇之乘與逆由正則函式提供。以範疇論描述,一個代數群是一個於代數簇範疇中的群對象。代數群(...
《李代數和代數群(英文)》中所討論的局部李群方法提供了求解非線性方程解析解通用且非常有效的方法,而近似變換群可以提高構造含少量參數的微分方程的技巧。《李代數...
《代數群引導》是2006年9月科學出版社出版的圖書,作者是黎景輝、陳志傑、趙春來。本書可供大學數學系學生、研究生、教師及相關的研究人員參考。...
在數學中,霍普夫代數是一類雙代數,亦即具有相容的結合代數與余代數結構的向量空間,配上一個對極映射,後者推廣了群上的逆元運算。霍普夫代數以數學家海因茨·霍普夫...
代數學、群與幾何(美)<Algebras,Groups andGeometries ) (Palm Harbor, FL ) 1984年創刊.刊號:513B0069, ISSN0074-9937.美國Hadronic出版公司出版、發行.季刊....
霍普夫代數是20世紀60年代以後迅速發展起來的代數學的新學科。域k上的霍普夫代數是同時具有k代數結構和它的對偶結構(k余代數結構)並滿足一定的相容條件的代數系統。...
在20世紀初,Fomin和Zelevinsky發明了一類新的代數,稱為簇代數。其動機是代數群中的總正性和量子群中的正則基。簇代數自問世以來,已在泊松幾何、泰克勒理論、...
《數學概覽:代數基本概念》是I.R.沙法列維奇的經典名著之一,目的是對代數學、它的基本概念和主要分支提供一個一般性的全面概述,論述代數學及其在現代數學和其他...
代數群是具有某種拓撲結構的群。代數群理論是群論與代數幾何學結合的產物,可以看成李群理論的推廣或者同李群理論平行的一個群論分支。外爾群是代數群的某種子群的商...
他也引入了代數群的概念,它在1950年之前並沒有被認真地發展過。 他也定義了反對稱微分形式的一般概念,以我們現在所使用的風格;他通過馬尤厄-嘉當方程處理李群的...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它...
無限群指元素個數為無限的群。拓撲群,李群,(無限)典型群,代數群,算術群,都是無限群。無限群的研究開始於19世紀下半葉。正當抽象群的概念形成之際,數學家們...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。伊代爾群(Idele group)是一種特殊的群。即各分量為諸局部域元素的...
在代數幾何中,一個概形S上的群概形G是範疇SchS中的群對象,具體定義請參見正文。...... 阿貝爾簇:即一個域k上的真(proper)代數群,它們必然是可交換的。...
拋物子群(parabolic subgroup)是代數群的一類閉子群。指代數群G的含有博雷爾子群的閉子群。若且唯若陪集空間G/P是完備簇,一個閉子群才是拋物子群。若P是簡約...
伴隨表示(adjoint representation)是代數群的一種表示,指代數群在它的李代數上的一個典範表示。設G是代數群,g是它的李代數,G在g上的伴隨表示定義為Ad:G→Aut(...
主要從事代數群與量子群領域研究。 現任中國科學院數學與系統科學研究院院長,中國科學院大學數學科學學院院長,中國數學會副理事長。 [1] ...
