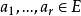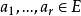基本介紹
發展歷程,基礎知識介紹,
發展歷程
早在19世紀初，伽羅華在研究代數方程的著作里就出現了域的概念的萌芽，後來戴德金(J.W.R.Dedekind)和克羅內克(L.Kronecker)在不同背景下也提出了域的概念。系統研究域的理論始於韋伯(H.Weber)，而域的公理系統是迪克森(L.E.Dickson)和亨廷頓(E.V.Huntington)分別於1903和1905年獨立創立的。在韋伯等人的影響下，施泰尼茨(E.Steinitz)對抽象域進行了系統研究，於1910年發表論文“域的代數理論”，對域論本身以及相關科學的發展產生重大影響。
1893年，安里西·韋伯給出抽象域的首個清晰定義。
1910年，施泰尼茨於1911年發表了論文《域的代數理論》（英文：Algebraic Theory of Fields、德文：Algebraische Theorie der Körper）。論文中他以公理化的方式研究了域的性質並給出了多個域的有關術語，比如素域、完全域，和域擴張的超越次數。
基礎知識介紹
一個交換除環稱域。即若F至少含有兩個元素，且有兩個代數運算+，·，F對+及F非零元集F*對·均為交換群，F對+滿足分配律。研究域的代數分支稱域論。一個含無窮多元素的域稱無限域；一個含有限個元素的域稱有限域或伽羅瓦域。由於域是交換單環，無真理想，因而域不能像群、環那樣，通過對不變子群，商群或理想、商環來討論。常用的方法是從已知域出發，研究它的擴域。
若F是E的子域，即E是F的擴域，記為E/F 。若E/F，且
，E的含F，
的最小子域記為F( )。為添加 於F所得的單擴域，且F( )={f( )/(ga)I g(a)≠o，f( )，g( )均為F上 的多項式}；若
，E的添加
於F的最小子域記為
。
若
，且存在多項式
使
，稱
為F上代數元，否則稱 為F上超越元；若E/F，且E中元均為F上代數元，則稱E是F的代數擴域；若
是F上代數元，則
是F的代數擴域，稱為F的單代數擴域，添加一個超越元所得擴域即為單超越擴域。單代數擴域與單超越擴域有不同的結構：若
為F上超越元，則
的商域；若
為F上代數元，則
，其中p(x)是F上首1的不可約多項式，且
時。稱p(x)為 在F上的極小多項式。並且若
， 則
。
給定擴域E/F，E作為F上向量空問，若
，稱n為E在F上的次數，記作(E：F)。若(E：F)有限，稱E為F上有限擴域，否則稱為無限擴域。若有域列
，且(E：I)，(I：F)皆有限，則(E：F)有限，且(E：F)=(E：I)(I：F)。一般，若
，且
有限(i=1，…，s)，則
有限，且
。單代數擴域
是F的有限擴域，若
在F上的極小多項式為p(x)，則
。並且F的每個有限擴域一定是F的代數擴域；若
均為F上代數元，則
是F的有限擴域，因而是代數擴域。
每一個次數大於0的數係數多項式在給定的數域上未必能分解成一次因式之積，但代數基本定理保證了每一個次數大於0的多項式在複數範圍都可分解為一次因式之積。如果F上每一個次數大於0的多項式均可分解為F上一次因式之積，稱F為代數閉域，此時F不再有真的代數擴域。每個域F均存在代數擴域E，使E為代數閉域；複數域是代數閉域。
若E是F的擴域，對於F上多項式f(x)，在E上f(x)可以分解為一次因式之積，並且對F的任一較小擴域I，f(x)在J上不能分解為一次因式之積，稱E為f(x)在F上的分裂域或根域。對於F上每個多項式，同構的意義下均存在唯一的分裂域。一個多項式的分裂域依賴於這個多項式係數所在的域，如
作為有理係數多項式，其分裂域為
，但作為實係數多項式，其分裂域仍為R。若
，
，在E上
，則
在F上分裂域
。
有限域是一類重要的域，有限域的特徵為素數。設F為特徵p的有限域，△為F的素子域，且(F：△)=n,則
，且F是
在△上分裂域。對任何素數p及正整數n，均存在
個元的有限域，且同構意義下唯一。有限域結構簡單：若F是有限域，△為F的素域，則存在F中
，
。有限域的非零元構成的乘群皆為循環群。若F*=(a)，則F=△( )。利用有限域的性質可以構造出各種對稱性質的組合結構，如正交拉丁方，平衡區組設計等，這些組合結構有效地套用於試驗設計，通信系統等許多實際領域中，特別隨著計算機技術蓬勃發展，有限域理論成了廣大工程技術人員不可缺少的數學工具。
