背景
日本著名的統計學家
田口玄一將正交試驗選擇的水平組合列成表格,稱為
正交表。例如作一個三因素三水平的實驗,按全面實驗要求,須進行3^3 = 27種組合的實驗,且尚未考慮每一組合的重複數。若按
L9(3)正交表安排實驗,只需作9次,按
L18(3)正交表進行18次實驗,顯然大大的減少了工作量。因而
正交實驗設計在很多領域的研究中已經得到廣泛套用。
正交表是一整套規則的設計表格,用 L為正交表的代號,n為試驗的次數,t為水平數,c為列數,也就是可能安排最多的因素個數。例如L9(3^4)它表示需作9次實驗,最多可觀察4個因素,每個因素均為3水平。一個
正交表中也可以各列的水平數不相等,我們稱它為混合型正交表,如L
8(4
1×2
4),此表的5列中,有1列是為4水平,4列為2水平。
設計表
正交試驗設計表
正交試驗因素水平表 正交試驗設計方案及試驗結果 極差分析表(或指標與因素關係圖)
方差分析表(簡單分析時可無)。
正交表的性質
(1)每一列中,不同的數字出現的次數是相等的。例如在兩水平
正交表中,任何一列都有數碼“1”與“2”,且任何一列中它們出現的次數是相等的;如在三水平正交表中,任何一列都有“1”、“2”、“3”,且在任一列的出現數均相等。
(2)任意兩列中數字的排列方式齊全而且均衡。例如在兩水平正交表中,任何兩列(同一橫行內)有序對子共有4種: (1,1)、(1,2)、(2,1)、(2,2)。每種對數出現次數相等。在三水平情況下,任何兩列(同一橫行內)
有序對共有9種,1.1、1.2、 1.3、2.1、2.2、2.3、3.1、3.2、3.3,且每對出現數也均相等。
以上兩點充分的體現了
正交表的兩大優越性,即“均勻分散性,整齊可比”。通俗的說,每個因素的每個水平與另一個因素各水平各碰一次,這就是
正交性。
正交表的獲得有專門的算法,對套用者來說,不必深究。
安排
正交試驗設計的關鍵在於試驗因素的安排。通常,在不考慮
互動作用的情況下,可以自由的將各個因素安排在
正交表的各列,只要不在同一列安排兩個因素即可(否則會出現混雜)。但是當要考慮互動作用時,就會受到一定的限制,如果任意安排,將會導致
互動效應與其它效應混雜的情況。
因素所在列是隨意的,但是一旦安排完成,試驗方案即確定,之後的試驗以及後續分析將根據這一安排進行,不能再改變。對於部分表,如L18(2*3^7)則沒有互動作用列,如果需要考慮互動作用需要選擇其它的正交表。
極差分析
在完成試驗收集完數據後,將要進行的是極差分析(也稱方差分析)。
極差分析就是在考慮A因素時,認為其它因素對結果的影響是均衡的,從而認為,A因素各水平的差異是由於A因素本身引起的。
用極差法分析正交試驗結果應引出以下幾個結論:
①在試驗範圍內,各列對
試驗指標的影響從大到小的排隊。
某列的極差最大,表示該列的數值在試驗範圍內變化時,使試驗指標數值的變化最大。所以各列對試驗指標的影響從大到小的排隊,就是各列極差D的數值從大到小的排隊。
②試驗指標隨各因素的變化趨勢。
③使試驗指標最好的適宜的操作條件(適宜的因素水平搭配)。
④對所得結論和進一步研究方向的討論。
條件選擇
各因素的好水平加在一起,是否就是較優試驗條件呢?理論上,如果各因素都不受其它因素的水平變動影響的,那么,把各因素的優水平簡單地組合起來就是較好試驗條件。但是,實際上選取較好生產條件時,還要考慮因素的主次,以便在同樣滿足指標要求的情況下,對於一些比較次要的因素按照優質、高產、低消耗的原則選取水平,得到更為結合試驗實際要求的較好生產條件。
以上介紹如何分析各因素水平的變動對指標的影響。討論A因素時,不管其它因素處在什麼水平,只從A的極差就可判斷它所起作用的大小。對其它因素也作同樣的分析,在此基礎上選取各因素的較優水平。
實踐中發現,有時不僅因素的水平變化對指標有影響,而且,有些因素間各水平的聯合指配對指標也產生影響,這種聯合搭配作用稱為互動作用。而互動作用應該在試驗設計時考慮到。
分析方法
直接對比法就是對試驗結果進行簡單的直接對比。直接對比法雖然對試驗結果給出了一定的說明,但是這個說明是定性的,而且不能肯定地告訴我們最佳的成分組合。顯然這種分析方法雖然簡單,但是不能令人滿意。
二、直觀分析法
直觀分析法是通過對每一因素的平均極差來分析問題。所謂極差就是平均效果中最大值和最小值的差。有了
極差,就可以找到影響指標的主要因素,並可以幫助我們找到最佳因素水平組合。
基本思想
考慮進行一個三因素、每個因素有三個水平的試驗。如果作全面試驗,需作3^3 = 27次。
若從27次試驗中選取一部分試驗,常將A和B分別固定在
A1和
B1水平上,與C的三個水平進行搭配,
A1
B1
C1,
A1
B1
C2,
A1
B1
C3。作完這3次試驗後,若
A1
B1
C3最優,則取定
C3這個水平,讓
A1和
C3固定,再分別與B因素的三個水平搭配,
A1
B2
C3,
A1
B3
C3。這2次試驗作完以後,若
A1
B2
C3最優,取定
B2,
C3這兩個水平,再作兩次試驗
A2
B2
C3,
A3
B2
C3,然後與一起比較,若
A3
B2
C3最優,則可斷言
A3
B2
C3是我們欲選取的最佳水平組合。這樣僅作了7次試驗就選出了最佳水平組合。
 正交試驗設計示意圖
正交試驗設計示意圖我們發現,這些試驗結果都分布在
立方體的一角,代表性較差,所以按上述方法選出的試驗水平組合併不是真正的最佳組合。
如果進行正交試驗設計,利用
正交表安排試驗,對於三因素三水平的試驗來說,需要作9次試驗,用“Δ”表示,標在圖中。如果每個平面都表示一個水平,共有九個平面,可以看到每個平面上都有三個“Δ”點,立方體的每條直線上都有一個“Δ”點,並且這些“Δ”點是均衡地分布著,因此這9次試驗的代表性很強,能較全面地反映出全面試驗的結果,這就是正交實驗設計所特有的均衡分散性。我們正是利用這一特性來合理的設計和安排試驗,以便通過儘可能少的試驗次數,找出最佳水平組合。
設計過程
1)確定試驗因素及水平數;
3)列出試驗方案及試驗結果;
4)對正交試驗設計結果進行分析,包括極差分析和
方差分析;
5)確定最優或較優因素水平組合。
正交試驗與遺傳算法的聯繫
(1)正交試驗設計法是遺傳算法的一種特例,即正交試驗設計法是一種初始種群固定的、只使用定向變異運算元的、只進化一代的遺傳算法。
(2)
遺傳算法的步驟比正交試驗設計法複雜,所需的試驗次數也要多於正交試驗設計法的試驗次數,但它產生的解要優於正交試驗設計法產生的解。
(3)遺傳算法的隱並行性使得它在處理
互動作用項時,效率比正交試驗設計法要高。
(4)正交試驗設計法可解決一般遺傳算法中的最小欺騙問題。
案例分析
案例:水稻播種機穴盤育秧播種裝置
水稻播種機穴盤育秧播種裝置的試驗設計
隨著栽培技術的不斷更新,高效、節本、高產的拋秧栽培法獲得了迅速發展和推廣。為了改善原有播種裝置中窩眼輥輪結構,我們研製成功了穴盤育秧播種裝置,它不僅解決了手工操作進行育秧培育的
勞動強度大,工作效率低等問題,而且能大幅度地提高播種量的穩定性和播種的
均勻性,使水稻播種機械更趨實用與完善。
(1)試驗目的 考慮影響播種性能的主要因素對水稻播種機穴盤育秧播種裝置播種性能的影響程度,以達到
最佳化設計參數。
(2)試驗條件 種子品種:雜交稻(協優46號)
種子狀況:經過脫芒、浸種、催芽露白、去雜質
秧盤規格:600mm×340mm,561穴
種子千粒重:26.9g
試驗盤數:100盤
秧盤運行速度與排種膠帶線速度嚴格一致。
(3)試驗因素
選用三個可變因素:
生產率(盤/小時)、播種量(粒/穴)、投種高度(mm)。
A.可變因素
B.可變的水平數每個因素分別取三個水平數
C.實驗因素與水平
為了研究生產率、播種量及投種高度對播種性能的影響,特安排了三因素三水平的正交試驗,試驗因素與水平見下表所示。
2.正交試驗方案與試驗結果分析
(1)正交試驗方案與試驗結果
選用
L9(34)
正交表進行試驗設計,試驗方案與試驗結果見下表所示。其數據採集方法為:在每種工況(每個試驗號)條件下進行
隨機抽樣3盤測定,測定播種合格率時,每盤隨機連片
抽樣100穴。最後,把3次測定的各項數據的平均值記入試驗結果。
 三次測試數據平均值
三次測試數據平均值(2)試驗結果分析如下表所示
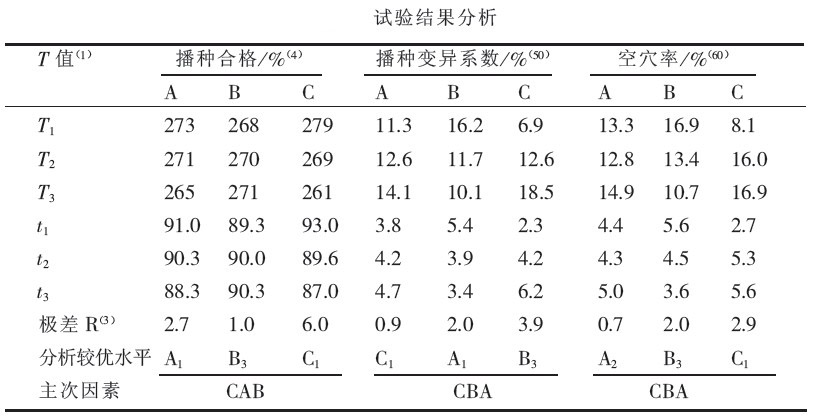 實驗結果分析
實驗結果分析註:
(1)T為因素試驗結果之和,如T1 = 93.0 + 91.0 + 89.0 = 273.0。
 實驗結果均值
實驗結果均值。
(3)R為t值中的大數-小數。
(4)播種合格率:每盤隨機測定的100穴,其中種子粒數合格的穴數所占的百分比(種子粒數合格範圍為:雜交稻(1-3粒/穴,常規稻3-6粒/穴)。
x——每盤播種量;
——平均盤播種量(g);
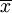 平均值
平均值n——試驗盤數,
 標準差
標準差(6)空穴率:每盤隨機測定的100穴,其中空穴數所占的百分比。
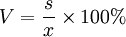 空穴率
空穴率由上面兩表得出影響3項指標的主次因素和較優水平為:播種合格率C1A1B3;播種變異係數C1B3A1;空穴率C1B3A2。
考慮到水稻播種的實際需要,經綜合分析,選取各試驗因素的較優水平組合為:A1B3C1、A2B3C1、A1B3C1。因為在上述正交試驗中未出現過A1B3C1以及A2B3C1,為此專門安排了單因素(生產量)三水平試驗,試驗結果見下表所示。
從上表可知,最佳組合為A2B3C1,播種合格率96.0%,播種變異係數1.9%,空穴率0.5%。
3.試驗結論 (1)400盤/小時是該播種裝置雜交稻播種的臨界生產率,高出此值,則各項性能指標受重大影響。
(2)播種量越大,各項性能指標越好。
(3)投種高度對播種質量的影響十分顯著,投種高度越低,播種質量越好。
 正交試驗設計示意圖
正交試驗設計示意圖 實驗結果分析
實驗結果分析 實驗結果均值
實驗結果均值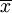 平均值
平均值 標準差
標準差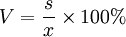 空穴率
空穴率
 三次測試數據平均值
三次測試數據平均值