正交試驗設計(Orthogonal experimental design)是研究多因素多水平的又一種設計方法,它是根據正交性從全面試驗中挑選出部分有代表性的點進行試驗,這些有代表性的點具備了“均勻分散,齊整可比”的特點,正交試驗設計是分式析因設計的主要方法。是一種高效率、快速、經濟的實驗設計方法。日本著名的統計學家田口玄一將正交試驗選擇的水平組合列成表格,稱為正交表。
當析因設計要求的實驗次數太多時,一個非常自然的想法就是從析因設計的水平組合中,選擇一部分有代表性水平組合進行試驗。因此就出現了分式析因設計(fractional factorial designs),但是對於試驗設計知識較少的實際工作者來說,選擇適當的分式析因設計還是比較困難的。 例如作一個三因素三水平的實驗,按全面實驗要求,須進行3^3=27種組合的實驗,且尚未考慮每一組合的重複數。若按L9(3^4)正交表安排實驗,只需作9次,按L15(3^7)正交表進行15次實驗,顯然大大減少了工作量。因而正交實驗設計在很多領域的研究中已經得到廣泛套用。
基本介紹
- 中文名:正交試驗
- 外文名:Orthogonal experimental design
- 類別:一種實驗設計方法
- 特點:“均勻分散,齊整可比”
基本思想
A:80-90℃
B:90-150分鐘
C:5-7%
試驗目的是搞清楚因子A、B、C對轉化率有什麼影響,哪些是主要的,哪些是次要的,從而確定最適生產條件,即溫度、時間及用鹼量各為多少才能使轉化率高。試製定試驗方案。
這裡,對因子A,在試驗範圍內選了三個水平;因子B和C也都取三個水平:
A:A1=80℃,A2=85℃,A3=90℃
B:B1=90分,B2=120分,B3=150分
C:C1=5%,C2=6%,C3=7%
當然,在正交試驗設計中,因子可以是定量的,也可以是定性的。而定量因子各水平間的距離可以相等,也可以不相等。
這個三因子三水平的條件試驗,通常有兩種試驗進行方法:
3^3=27次
試驗。用圖表示就是圖1 立方體的27個節點。這種試驗法叫做全面試驗法。
全面試驗對各因子與指標間的關係剖析得比較清楚。但試驗次數太多。特別是當因子數目多,每個因子的水平數目也多時。試驗量大得驚人。如選六個因子,每個因子取五個水平時,如欲做全面試驗,則需5^6=15625次試驗,這實際上是不可能實現的。如果套用正交實驗法,只做25次試驗就行了。而且在某種意義上講,這25次試驗代表了15625次試驗。圖1 全面試驗法取點。
 圖1
圖1B1C1 →A2
↘A3 (好結果)
如得出結果A3最好,則固定A於A3,C還是C1,使B變化之:
↗B1
A3C1 →B2 (好結果)
↘B3
得出結果以B2為最好,則固定B於B2,A於A3,使C變化之:
↗C1
A3B2→C2 (好結果)
↘C3
 圖2
圖2這種方法一般也有一定的效果,但缺點很多。首先這種方法的選點代表性很差,如按上述方法進行試驗,試驗點完全分布在一個角上,而在一個很大的範圍內沒有選點。因此這種試驗方法不全面,所選的工藝條件A3B2C2不一定是27個組合中最好的。其次,用這種方法比較條件好壞時,是把單個的試驗數據拿來,進行數值上的簡單比較,而試驗數據中必然要包含著誤差成分,所以單個數據的簡單比較不能剔除誤差的干擾,必然造成結論的不穩定。
簡單對比法的最大優點就是試驗次數少,例如六因子五水平試驗,在不重複時,只用5+(6-1)×(5-1)=5+5×4=25次試驗就可以了。
當因子數和水平數都不太大時,尚可通過作圖的辦法來選擇分布很均勻的試驗點。但是因子數和水平數多了,作圖的方法就不行了。
試驗工作者在長期的工作中總結出一套辦法,創造出所謂的正交表。按照正交表來安排試驗,既能使試驗點分布得很均勻,又能減少試驗次數,圖2正交試驗設計圖例而且計算分析簡單,能夠清晰地闡明試驗條件與指標之間的關係。用正交表來安排試驗及分析試驗結果,這種方法叫正交試驗設計法。


正交表




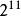
L8(

7為此表列的數目(最多可安排的因子數)
2為因子的水平數
8為此表行的數目(試驗次數)
L16(2×
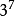
有7列是3水平的
有1列是2水平的
L16(2×

在行數為mn型的正交表中(m,n是正整數),試驗次數(行數)=Σ(每列水平數-1)+ 1
如L8(

8=7×(2-1)+l
利用上述關係式可以從所要考察的因子水平數來決定最低的試驗次數,進而選擇合適的正交表。比如要考察五個3水平因子及一個2水平因子,則起碼的試驗次數為5×(3-1)+1×(2-1)+1=12(次)
這就是說,要在行數不小於13,既有2水平列又有3水平列的正交表中選擇,L18(2×
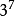
正交表具有兩條性質:(1)每一列中各數字出現的次數都一樣多。(2)任何兩列所構成的各有序數對出現的次數都一樣多。所以稱之謂正交表。
例如在L9(

 表1
表1方案設計
3×(3-1)+1=7(次)
可考慮選用L9(


 表2
表2
再看一個用L9(

[例2]某礦物氣體還原試驗中,要考慮還原時間(A)、還原溫度(B)、氣體流速(C)、還原氣體比例(D)這四個因子對全鐵含量X〔越高越好)、金屬化率Y(越高越好)、二氧化鈦含量Z(越低越好)這三項指標的影響。希望通過試驗找出主要影響因素,確定最適工藝條件。
首先根據專業知識以確定各因子的水平:
時間:A1=3(小時),A2=4(小時),A3=5(小時)
溫度:B1=1000(℃),B2=1100(℃),B3=1200(℃)
流速:Cl=600(毫升/分),C2=400(毫升/分),
C3=800(毫升/分)
CO:H2:D1=1:2,D2=2:1,D3=1:1
這是四因子3水平的多指標(X、Y、Z)問題,如果做全面試驗需3^4=81次試驗,而用L9(

 表3
表3數據分析


第二類收穫是認識和展望。9次試驗在全體可能的條件中(遠不止3^3=27個組合,在試驗範圍內還可以取更多的水平組合)只是一小部分,所以還可能擴大。精益求精。尋求更好的條件。利用正交表的計算分折,分辨出主次因素,預測更好的水平組合,為進一步的試驗提供有份量的依據。
其中I、Ⅱ、Ⅲ分別為各對應列(因子)上1、2、3水平效應的估計值,其計算式是:
Ⅰi(Ⅱi,Ⅲi)=第i列上對應水平1(2,3)的數據和
K1 為1水平數據的綜合平均=Ⅰ/水平1的重複次數
Si為變動平方和=
[例1]的轉化率試驗數據與計算分析見表4。
先考慮溫度對轉比率的影響。但單個拿出不同溫度的數據是不能比較的,因為造成數據差異的原因除溫度外還有其他因素。但從整體上看,80℃時三種反應時間和三種用鹼量全遇到了,85℃時、90℃時也是如此。這樣,對於每種溫度下的三個數據的綜合數來說,反應時間與加鹼量處於完全平等狀態,這時溫度就具有可比性。所以算得三個溫度下三次試驗的轉化率之和:
80℃: ⅠA=x1+x2+x3=31+54+38=123;
85℃: ⅡA=x4+x5+x6=53+49+42=144;
90℃: ⅢA=x7+x8+x9=57+62+64=183。
分別填在A列下的Ⅰ、Ⅱ、Ⅲ三行。再分別除以3,表示80℃、85℃、90℃時綜合平均意義下的轉化率,填入下三行K1、K2、K3。R行稱為極差,表明因子對結果的影響幅度。
同樣地,為了比較反應時間;用鹼量對轉化率的影響,也先算出同一水平下的數據和IB、ⅡB、ⅢB,IC、ⅡC、ⅢC,再計算其平均值和極差。都填入表4中;
由此分別得出結論:溫度越高轉化率越好,以90℃為最好,但可以進一步探索溫度更好的情況。反應時間以120分轉化率最高。用鹼量以6%轉化率最高。所以最適水平是A3B2C2。
(1)設假設H0正確,得到一個理論結論,設此結論為R0;
(2)再根據試驗得出一個試驗結論,與理論結論相對應,設為R1;
(3)比較R0與R1:若R0與R1沒有大的差異,則沒有理由懷疑H0,從而判定為:"不捨棄H。"(採用H。);若R0與R1有較大差異,則可以懷疑H0,此時判定為:"捨棄H0"。
但是,R1/R0比值為多少才能捨棄H0呢?為確定這個量的界限,需要利用數理統計中F分布的理論。
若yl服從自由度為φ1的χ2分布,y2服從自由度為φ2的χ2分布,並且yl、y2相互獨立,則(y1/φ1)/(y2/φ2)服從自由度為(φ1,φ2)的F分布。F分布是連續分布,分布模數是兩個自由度(φ1,φ2)。稱φ1為分子自由度,稱φ2為分母自由度。在自由度為(φ1,φ2)的F分布中,某點右側面積為p,也就是F比此值大的機率為p,把這個值寫為 (p)。若檢驗的顯著性水平(或危險率)給定為α時,則可以把 (α)作為臨界值來檢驗假設。
這裡,Se/σ2服從自由度為φe,的χ2分布;當H。成立,σ2=0時,SA/σ2也服從自由度為φA的χ2分布;又SA與Se相互成立,所以(SA/(φAσ2)/ Se/(φeσ2))=VA/Ve服從自由度為(φA,φe)的F分布。這就是假定H。正確時的理論結論R。。而試驗結論Rl要與理論結論R。相比較。由給定的顯著性水平,通常是α=0.05;分子自由度φ1=φA=a-1,分母自由度φ2=φe=a(n-1);查F分布表得出 (α)。所以H。:α1=α2=……=αa=0(σA2=0)的檢驗是:(顯著性水平α)
FA=VA/Ve> (α) → 捨棄H0;
FA=VA/Ve≤ (α) → 不捨棄H0;
通常, (α)一般性地表示成Fα(φA,φB)。
假設因子A對試驗結果的影響不顯著,那么A的兩個水平的效應該表現為相等或相近,即假設H0:α1=α2=0。如果因子A顯著,則捨棄假設。
為了判斷因子A是否顯著,首先要計算比值顯然,這個比值越大,因子A對指標的影響越顯著;反之,因子A就不顯著。在給定置信度α後,如α=0.05,查F分布表,自由度φA是因子A的,自由度φe是誤差的,其臨界值Fα(φA,φe),如果FA>Fα(φA,φe)就捨棄假設,可以認為因子A是顯著的;如果FA≤Fα(φA,φe)就沒有理由否定假設,而只能認為因子A是不顯著的。因為按照F分布表的物理念義,F值小於Fα(φA,φe)的機率是95%,即有95%的機會出現小於Fα(φA,φe)的F值,既然出現了這種情況,就有了95%的把握,所以就沒有理由否定假設,只能接受假設,認為因子A不顯著。另一方面,F值大於Fα(φA,φe)的機率是5%,也就是只有5%的機會出現大於Fα(φA,φe)的F值,這是小機率事件,如果小機率事件居然發生了,則可認為情況異常,假設不可信,必須否定假設,因子A是顯著的。對其他因子的顯著性檢驗完全類似。
(二)方差分析表
由總平方和與各因素平方和即可求得誤差平方和,亦稱剩餘平方和。是總平方和減各因素平方和所得。如正交表有一空列,則該列的平方和就是誤差平方和。但在正交表飽和試驗的情況下,即所有各列全部排滿時,誤差平方和一般用各因素平方和中幾個最小的平方和之和來代替,同時,這幾個因素不再作進一步的分析。
自由度:φT=試驗次數一1
φA,B…=水平數一1
φA×B=φA×φB
φe=φT-φA-φB-……-φD
 表5
表5
