基本介紹
- 中文名:域擴張
- 外文名:field extensions
- 領域:數學
- 套用:抽象代數
定義
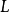
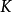
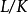
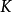
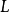
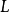
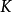
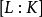
基本性質
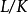
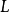
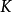
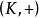
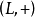
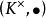
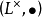

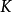
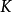
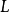
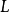
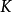
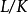
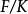
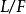
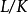
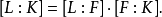
代數元與超越元
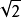
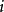
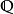
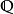
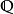
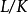
例子
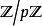
正規、可分與伽羅瓦擴張
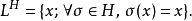
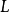
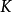
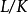
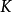
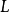
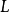
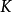
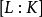
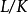
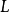
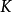
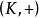
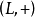
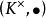
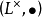

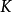
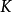
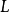
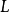
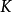
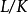
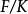
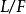
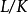
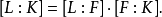
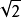
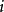
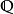
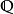
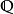
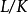
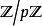
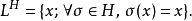
域擴張(field extensions)是數學分支抽象代數之域論中的主要研究對象,基本想法是從一個基域開始以某種方式構造包含它的“更大”的域。域擴張可以推廣為環擴張。...
二次擴張(quadratic extension)是一類重要的有限擴張。二次擴張是指擴張次數為2的域擴張。域F上的二次不可約多項式的分裂域是F的二次擴張。設K/F是域擴張,K′...
庫默爾擴張是(Kummer extesion)是阿貝爾擴張的一種類型。因首先由E.E.庫默爾研究而得名。阿貝爾擴張是代數數論研究的主要對象。...
伽羅瓦擴張:在數學中,如果一個域擴張 K/k 既是一個正規擴張又是可分擴張,那 K/k 就是一個伽羅瓦擴張。注意正規擴張隱含了 K/k 是一個代數擴張。...
模擴張(modular extension)是比可分擴張更廣泛的一類域擴張。特徵為p≠0的域擴張K/F,若對於每個整數n≥1,K與F都是線性分離的,則稱為模擴張。可分擴張就是模...
純量擴張(scalar extension)是常用的代數基域擴張,它對域上中心單代數結構的研究有重要作用。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F...
擴張次數(degree of extension)決定擴域結構的一個數.設E是F的擴域,E作為F上向量空間的維數稱為此域擴張的次數,記為[E " F'].當[E " F]<二時,稱此...
阿貝爾擴張(Abelian extension)是一類重要的域擴張,設K是域F的伽羅瓦擴域,若其伽羅瓦群G(K/F)為一阿貝爾群,則稱此擴張為阿貝爾擴張,此時,K稱為F上阿貝爾擴域...
希爾伯特類域(Hilbert class field)亦稱最大非分歧阿貝爾擴張。一種重要的類域。最早由希爾伯特(Hilbert,D.)於1898年至1899年猜出,後來發展為系統而一般的類域論...
種域(genus field)是類域的一種重要的子域。數域K的種域K定義為K的最大的如下阿貝爾擴張,它是K與一個絕對阿貝爾域K1的複合,且在K的素除子上均不分歧。...
有理函式域(rational function field)是一種重要的純超越擴張。純超越擴張是一類重要的超越擴張。設擴域K在F上的超越基為S,若K=F(S),則稱此域擴張為純超越...
域多項式(field polynomial)一種特殊多項式.指在域擴張下,由一個元素所決定的多項式一個有限域擴張K/F,K可以看成F上的有限維向量空間.設w是它的一個基,對於x...
域論(Field Theory)是抽象代數的分支,是不少學科的基礎,是代數學中最基本的概念之一,且歷史悠久。研究域的性質,簡單地說,一個域是在其上有"加法"、"減法"、...
共軛域(conjugate fields)是一種同構擴域。設L是域F的擴域,E,E′為其兩個中間域,若存在一個F共軛映射σ使σ(E)=E′,則稱E與E′是F上在L內的共軛域。...
代數數域是數學中代數數論的基本概念,數域的一類,有時也被簡稱為數域,指有理數域 ℚ 的有限擴張形成的擴域。任何代數數域都可以視作 ℚ 上的有限維向量...
滲透型擴張戰略是指企業在現有區域周邊逐步滲透式地開拓經營區域,在現有經營區域穩固的基礎上,再尋找另外比較接近的區域進行拓展,以便充分挖掘周邊區域市場潛力,發揮...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。而伽羅瓦群(Groupe de Galois)是與某個類型的域擴張相伴的群。是...
