基本介紹
- 中文名:代數數域
- 外文名:algebraic number field
- 適用範圍:數理科學
簡介
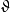
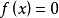
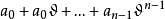
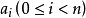
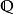
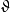
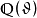
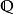
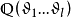
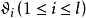
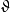
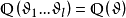
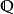
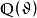
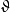
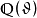
舉例


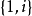


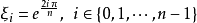

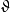
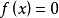
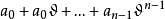
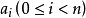
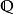
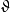
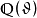
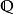
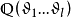
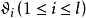
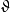
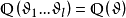
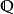
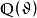
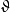
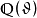


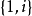


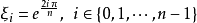
代數數域是數學中代數數論的基本概念,數域的一類,有時也被簡稱為數域,指有理數域 ℚ 的有限擴張形成的擴域。任何代數數域都可以視作 ℚ 上的有限維向量...
代數數是代數與數論中的重要概念,指任何整係數多項式的復根。所有代數數的集合構成一個域,稱為代數數域。不是代數數的實數稱為超越數,例如圓周率。...
設P是由一些複數組成的集合,其中包括0與1,如果P中任意兩個數的和、差、積、商(除數不為0)仍是P中的數,則稱P為一個數域。常見數域: 復數域C;實數域R;...
P 進數域又稱局部數域,它是數域關於進絕對值的完備化。進數域的研究和代數數論的局部化方法,均始於K.亨澤爾1902年的工作。...
代數整數環(ring of algebraic integers)亦稱整數環,是一種特殊的交換整環,代數數域K中的代數整數全體OK稱為K的整數環,K是OK的商域,設L⊃K是兩個數域,則...
域F稱為代數閉域,如果對於任何係數屬於F的一元多項式f(x),f(x)在F中至少有一個根。...... 域F稱為代數閉域,如果對於任何係數屬於F的一元多項式f(x),f(...
P進數域是一類特殊的局部域。設局部域K的特徵數為𝓀,當K為∞時,K是伽羅瓦域GF(pc)上的p進數域(c=1),或是p進數的有限次代數擴張;這裡p為素數。...
若V是域k上的代數簇,則RatR(V)稱為V的函式域。設f是X到Y的有理映射,如果存在(U,φ)∈f,使得φ(U)是Y的稠密子集,則稱f是控制的。設V,W是代數簇,...
域論是代數數論的重要理論之一。它深刻地刻畫了(相對)阿貝爾擴張。代數元(algebraic element)是域論的基本概念之一。設K是域F的擴域,K中元α稱為F上代數元,是...
域論(Field Theory)是抽象代數的分支,是不少學科的基礎,是代數學中最基本的概念之一,且歷史悠久。研究域的性質,簡單地說,一個域是在其上有"加法"、"減法"、...
域上代數相關集(algebraically dependent setover a field)是與超越基密切相關的一個概念。設K是F的域擴張,S是K的子集。若y∈K是F(S)上的代數元,則稱y在F...
《代數數理論講義》是2005年科學出版社出版的圖書,作者是赫克。...... 的簡化;給出了任意代數數域中最一般二次互反律一個新的證明,並給出了相對二次類域存在...
域是代數學的基本概念之一。即具有兩個運算的代數系。設F是至少含兩個元的集合,在F中定義了兩個二元運算:一個稱加法,使F成為加群,它的單位元稱為F的零元;...
所謂霍普夫代數,是指一個域上的雙代數,配上一個線性映射 (稱為對極映射),使得下述圖一表交換。利用Sweedler 記號,此定義亦可表為對極映射可理解為 對卷積之逆...
域的特徵是交換代數中的基本概念。 一個域就是滿足加、減、乘、除 四則運算的集合。 比如有理數域, 有理函式域, 代數數域、伽羅華域等等。...
種域(genus field)是類域的一種重要的子域。數域K的種域K定義為K的最大的如下阿貝爾擴張,它是K與一個絕對阿貝爾域K1的複合,且在K的素除子上均不分歧。...
域擴張(field extensions)是數學分支抽象代數之域論中的主要研究對象,基本想法是從一個基域開始以某種方式構造包含它的“更大”的域。域擴張可以推廣為環擴張。...
代數數論的重要理論之一。它深刻地刻畫了(相對)阿貝爾擴張.基本定理如下:若K/k為數域的有限阿貝爾擴張,伽羅瓦群為G=G(K/k),則存在k的模f(稱為K/k的導子...
整體域(global field)通常指代數數域和有限常數域上單變數代數函式域.這是相對於局部域而言。...
