域是代數學的基本概念之一。即具有兩個運算的代數系。設F是至少含兩個元的集合,在F中定義了兩個二元運算:一個稱加法,使F成為加群,它的單位元稱為F的零元;一個稱乘法,使F的非零元構成一個交換群,加法與乘法滿足分配律,此時稱F為域。
擬代數閉域(quasi-algebraically closed field)是一類特殊的域。C1域的舊稱,始用於20世紀30年代。
基本介紹
- 中文名:擬代數閉域
- 外文名:quasi-algebraically closed field
- 領域:數學
- 性質:特殊的域
- 方式:域的擴張
- 相關術語:代數閉域
概念,域,實閉域,代數閉域,域的擴張,代數擴張,
概念
擬代數閉域(quasi-algebraically closed field)是一類特殊的域。C1域的舊稱,始用於20世紀30年代。這個名稱的涵義可由下述事實認知:擬代數閉域的任何代數擴張仍為擬代數閉域。有限域是擬代數閉域(謝瓦萊定理)。代數閉域上的單元代數函式域是擬代數閉域(曾炯之定理,簡稱曾定理)。
域
域是代數學的基本概念之一。即具有兩個運算的代數系。設F是至少含兩個元的集合,在F中定義了兩個二元運算:一個稱加法,使F成為加群,它的單位元稱為F的零元;一個稱乘法,使F的非零元構成一個交換群,加法與乘法滿足分配律,此時稱F為域。例如,全體有理數、全體實數和全體複數在通常的加法與乘法下都構成域,分別稱為有理數域、實數域和複數域。域是許多數學分支研究的基礎,尤其對代數、代數數論、代數幾何等更為重要。可交換的除環叫做域,它是代數學的基本概念之一。
域的概念在19世紀代數學的發展中逐步形成並明確起來。在伽羅瓦的著作中就包含了域的概念,他的域就是由方程的係數生成的域,他的擴域是經添加方程的一個根作成的。在拉格朗日關於群論的論文和高斯關於數論的論文中也有了域的思想。域的概念是在克羅內克和戴德金關於代數數的論文中,從不同角度引入的。戴德金把他所引入的域的概念最初稱為“有理區域”,他關於域的理論發表在對狄利克雷《數論講義》一書所作的評註和附錄中。他在那裡從本質上補充並擴展了數論、理想論和有限域論。“域”這個術語首次出現在該書1871年的版本中。在19世紀,已經知道的具體的域有:有理數域、實數域、複數域、代數數域和有理函式域。1908年,德國數學家亨澤爾又引進了一類p-進域,並進行了系統研究。
域的抽象理論開始於德國數學家韋伯的工作。1893年他曾給伽羅瓦理論以抽象的闡述,其中引進域的概念作為群的派生,並強調群和域是代數的兩個主要概念。1903年美國數學家迪克森和亨廷頓建立了一個獨立的域的公理體系。
德國數學家施泰尼茨在韋伯的工作的影響下,對抽象域進行了綜合研究。按照他的觀點,每一個域都可以從它的素域(所有子域的公共元素所構成的子域)出發,經過適當的添加而得到。由此引進了代數擴張和域的特徵的概念。他還研究了伽羅瓦方程理論在域中的有效性問題。他的研究成果都包含在他寫於1910年的論文《域的代數理論》中。
19世紀末到20世紀初,美國數學家得到有限域的一些結果,如有限抽象域都與某一個伽羅瓦域同構(穆爾,1893);任何有限域必須是交換的(韋德伯恩、迪克森,1905)等等。
20世紀以來,對抽象域的研究又有新的進展,中國數學家曾炯之做出了一定貢獻。
實閉域
實閉域是一類重要的實域。設F是一個實域,若F的任何真代數擴張都不再是實域,則稱F是實閉的,或者F是一個實閉域。實閉域的例子很多,最常見的是:實數域R;由所有實代數數所成的域RAlg。實閉域只有惟一的序>,它由a>0若且唯若a=b所確定,換言之,它的惟一的正錐是由所有平方元所組成。在實閉域上,任何一元多項式都能表為一次與二次不可約因式之積。實閉域與代數閉域間的緊密關係,可以從下面的事實認知:設Ω是一個代數閉域,F是它的真子域。若Ω/F是有限擴張,則F是實閉域,並且有Ω=F(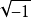 )。實閉域還有一個重要性質:任何一條初等的代數命題,若在某一個實閉域上成立,則必然在所有的實閉域上成立。這個結論被稱為塔爾斯基(Tarski,A.)原則(或定理)。根據這個原則,凡在實數域R上成立的初等代數命題,在任何實閉域上也成立。
)。實閉域還有一個重要性質:任何一條初等的代數命題,若在某一個實閉域上成立,則必然在所有的實閉域上成立。這個結論被稱為塔爾斯基(Tarski,A.)原則(或定理)。根據這個原則,凡在實數域R上成立的初等代數命題,在任何實閉域上也成立。
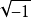
代數閉域
代數閉域是一類重要的域。指次數大於1的多項式均可分解的域。若域K上多項式環K[x]中的每一個次數大於零的多項式在K中都有一個根,則稱K為代數閉域。從而在K[x]中每個次數大於零的多項式能分解為一次因式之積。1910年,施泰尼茨(Steinitz,E.)在他發表的基本論文中首先證明:每個域都可以經代數擴張得到一個代數閉域。
域的擴張
域的擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。
若域E是F的擴域,K是E的擴域,則稱E是域擴張K/F的中間域。若K/F是域擴張,S是K的子集,且F(S)是K的含F與S的最小子域,稱F(S)為F添加S的擴域。當S={α1,α2,…,αn}是有限集合時,F(α1,α2,…,αn)稱為添加α1,α2,…,αn於F的有限生成擴域(或者F上的有限生成擴張)。它由一切形如:
f(α1,α2,…,αn)/g(α1,α2,…,αn)
的元組成,其中α1,α2,…,αn∈S,f,g是F上的n元多項式且:
g(α1,α2,…,αn)≠0.
由於這個原因,當F(α1,α2,…,αn)關於F的超越次數≥1時,F(α1,α2,…,αn)也稱為F上的代數函式域。當S={α}時,稱F(α)為F的單擴張域,也稱本原擴域。F的有限代數擴域K是單擴域的充分必要條件是,擴域K與基域間存在有限箇中間域.這是施泰尼茨(Steinitz,E.)證明的。
代數擴張
代數擴張是一類重要的域擴張。設E是F的擴域,若E中元皆為F上的代數元,則稱此域擴張為代數擴張,E稱為F的代數擴域,否則稱為超越擴張,而E稱為F的超越擴域.代數擴張具有傳遞性。當α是F上代數元時,其單代數擴域F(α)同構於F[x]/(p(x)),p(x)是α的最小多項式,(p(x))表F[x]中由p(x)生成的主理想。
