二次域,就是有理數域Q的二次擴域。每個二次域都可表示成其中d 不等於1是無平方因子的有理整數,按照d>0和d<0,分別稱K為實二次域和虛二次域。二次域是除了有理數域之外最簡單的一類代數數域。它有較簡單的數學結構和特性。
基本介紹
- 中文名:二次域
- 外文名:quadratic field
- 適用範圍:數理科學
定義,發展,
定義
假定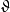 適合一個有理整係數的既約二次方程。則
適合一個有理整係數的既約二次方程。則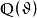 就稱為一個二次域。實際上,全體二次域即
就稱為一個二次域。實際上,全體二次域即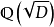 ,其中 D 過所有不等於 1 且無平方因子的有理整數。
,其中 D 過所有不等於 1 且無平方因子的有理整數。
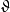
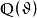
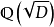
當 D>0 時,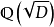 稱為實二次域(real quadratic field);
稱為實二次域(real quadratic field);
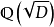
當 D<0 時,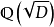 稱為虛二次域(imaginary quaadratic field);
稱為虛二次域(imaginary quaadratic field);
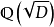
當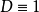 (mod 4)時,命
(mod 4)時,命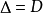 及
及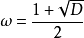 ;
;
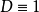
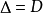
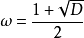
當 (mod 4)時,命
(mod 4)時,命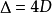 及
及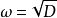 。則
。則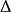 為
為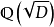 的判別式,而1、
的判別式,而1、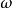 為
為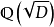 的一組整基。1、
的一組整基。1、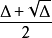 亦為
亦為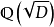 的一組整基。
的一組整基。

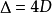
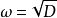
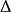
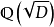
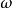
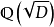
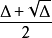
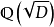
發展
1801年,C.F.高斯發表了他在20歲時所寫的數論著作《算術研究》,展現了他的一個傑出的思想,即把有理數域和有理整數環上的許多初等數論問題,放到更大的域和環──二次域和它的(代數)整數環上來研究。他在這些方面的工作,是研究二次域的開端,也是代數數論的一個源頭。
二次域有許多研究課題,其中最著名的是高斯關於類數問題的兩個猜想:
①只有有限多個類數為1的虛二次域;
②存在著無限多個類數為1的實二次域。
關於第一個猜想,1934年,H.海布雷恩給出了初步證明。1935年C.L.西格爾進一步證明了該猜想。A.貝克於1966年和H.M.斯塔爾克於1967年各自獨立地證明了類數為1的虛二次域只有9個:d=1,2,3,7,11,19,43,67,163。至於第二個猜想,則至今仍未解決。

