P進數域是一類特殊的局部域。設局部域K的特徵數為𝓀,當K為∞時,K是伽羅瓦域GF(pc)上的p進數域(c=1),或是p進數的有限次代數擴張;這裡p為素數。
基本介紹
- 中文名:P進數域
- 外文名:p-adic number field
- 適用範圍:數理科學
簡介
模
p級數域
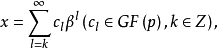
p進數域
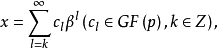
P進數域是一類特殊的局部域。設局部域K的特徵數為𝓀,當K為∞時,K是伽羅瓦域GF(pc)上的p進數域(c=1),或是p進數的有限次代數擴張;這裡p為素數。
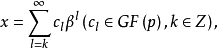
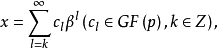
P進數域是一類特殊的局部域。設局部域K的特徵數為𝓀,當K為∞時,K是伽羅瓦域GF(pc)上的p進數域(c=1),或是p進數的有限次代數擴張;這裡p為素數。...
p進數是數論中的概念,也稱作局部數域,是有理數域拓展成的完備數域的一種。p進數的概念首先由庫爾特·亨澤爾於1897年構思並刻畫,其發展動機主要是試圖將冪級數...
p進數分析是研究變數為p進數的函式之,屬於數論研究中的領域。 ...... p進數域是有理數域裝備了與歐幾里德範數不同的p進範數後進行拓撲完備化得到的完備數域,...
《P進數,P進分析和ζ函式》是2009年6月世界圖書出版公司出版的圖書,作者是科比利茲。本書可供數學係數論專業的研究生和研究人員參考。...
的有限擴張也稱為代數數域,在代數數論有重要地位。有理數的另一個擴張域是關於一個素數p的p進數域 。它與 類似,是有理數域完備化得到的數域。但由於使用的...
通常將域F取為實數域R、複數域C或非阿基米德局部域,如p進數域 。此時辛群Sp(2n,F)是維度等於 的連通代數群。 是單連通的,而 的基本群則同構於 。...
他吸取亨澤爾P進數以及局部一全局思想,提出局部一全局原理(後稱哈塞原理),並利用這個原理解決了二次型的有理等價問題。之後他用同樣的方法研究代數數域問題,證明了...
連續幾何.代數閉域上有限秩的半單代數.對有限群表示的套用. 第11節 有限秩的可除代數 R或有限域上的有限秩可除代數.Tsen定理和擬代數閉域.p進數 域和...
《數論1:Fermat的夢想和類域論》起點低,但內容豐富,包括了現代數論的基本知識,如:橢圓曲線、p進數、代數數域、局部-整體方法等。...
在抽象代數中,交換代數旨在探討交換環及其理想,以及交換環上的模。代數數論與代數幾何皆奠基於交換代數。交換環中最突出的例子包括多項式環、代數整數環與p進數環,...
那么在 ℚ 內是代數獨立的;也就是說,擴張域在 ℚ 內具有超越...p進數林德曼-魏爾斯特拉斯猜想,就是這個定理在p進數中也成立:假設p是素數,...
