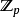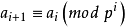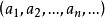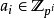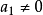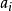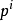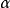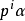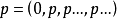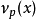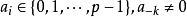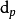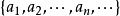基本介紹
- 中文名:p進數
- 外文名:p-adic numbers
- 提出者:Kurt Hensel
- 提出時間:1897年
- 套用學科:數論
- 適用領域範圍:量子物理學、認知科學、計算機科學
- 推廣:實數和複數的(普通)絕對值概念
定義,展開式,記數法,例子,套用,數論,量子物理,信息編碼,動力系統理論,
定義
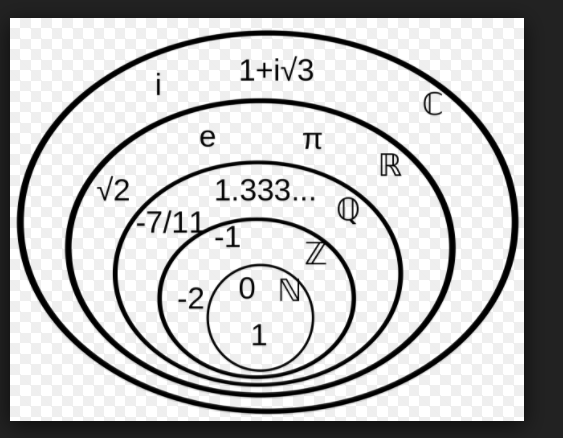
p-adic numbers由Kurt Hensel在1908年首先引入。對每個質數p, p進數系統將有理數的普通算術用一種不同於實數和複數系統的方法進行了擴展。這是通過對絕對值這一概念的另一種解釋來達成的。p進數主要是被一次將冪級數的思想和技術引入到數論中的嘗試所推動,但它們現在的影響不止於此。例如,p進數分析這一領域實際上提供了另一種形式的微積分。
更精確的講,給定一個質數p,p進數的域 Qp是有理數的擴展. 把所有Qp域放在一起考量,我們就有了Helmut Hasse的局部-全體原則, 該原則大意是特定方程組在有理數上有解若且唯若它們在實數上和所有質數p的p進數上有解。域 Qp也是一個度量拓撲空間,該度量由有理數的另一種取值導出。該度量是完備的(每個柯西列收斂).這使得Qp上能引入微積分,這個分析和代數結構的互動影響給了p進數系統其價值和用途。

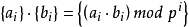
此時所有的p進整數構成含麼交換環,其零元與單位元分別為全零和全一的p進整數。
由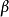 不為零知,存在最小的i使得
不為零知,存在最小的i使得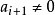 ,那么由定義知
,那么由定義知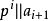 。由歸納法易知
。由歸納法易知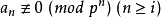 且
且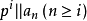 ,因此
,因此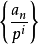 將是可逆的,容易驗證
將是可逆的,容易驗證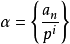 。
。
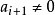
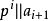
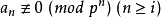
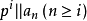
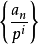
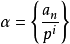
有了如上性質我們可以定義p進有理數為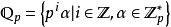 ,容易驗證
,容易驗證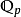 構成域且為
構成域且為 的分式域。事實上通過指數i我們可以定義
的分式域。事實上通過指數i我們可以定義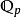 的賦值為
的賦值為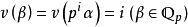 ,因此
,因此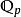 構成賦值域。
構成賦值域。
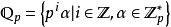

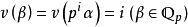
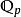
展開式
每個p進數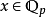 都有唯一的展開式:
都有唯一的展開式:
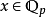
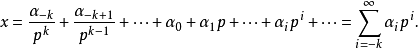
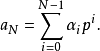
這說明p進整數數列表示中,隨著項數增大,數列的項在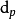 下收斂到p進整數自身。
下收斂到p進整數自身。
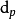
記數法
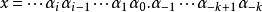
稱為p進數的p進記法。
按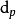 的定義,x的“大小”(範數)為
的定義,x的“大小”(範數)為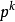 。也就是說,一個p進數小數點後位數越多則越大。這個性質與實數正好相反。
。也就是說,一個p進數小數點後位數越多則越大。這個性質與實數正好相反。
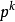
例子
從代數構造方法中可知,整數Z可以自然地嵌入Zp中,因此非負整數在Qp中表現為有限位數的p進整數。其p進記法和p進制記數法雷同。例如當 p=5時,自然數 438記為: 32235。負整數和分母不為p的正整數次冪的分數在p進記法中則表現為向左側延伸的無限循環。例如 的p進記法為:
的p進記法為:

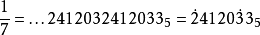
計算方法如下:
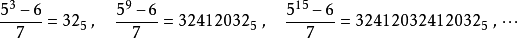
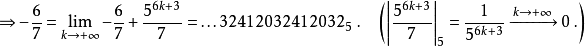
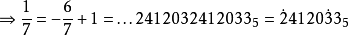
如果有理數x的分子或分母里含有p的冪次,則可以仿照p進制記數法的做法,先將其提出作為因數,寫成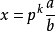 的形式,將
的形式,將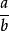 表達為p進記法,然後移動小數點得到x的p進記法。例如要求
表達為p進記法,然後移動小數點得到x的p進記法。例如要求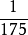 的p進記法,可以先將
的p進記法,可以先將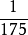 表示為
表示為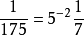 ,寫出
,寫出 的p進記法後,將小數點向左移動兩位得到:
的p進記法後,將小數點向左移動兩位得到:
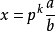
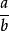
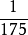
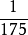
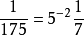

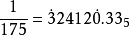
因此,分母為p的正整數次冪的分數在p進數中表現為有限小數。
套用
數論
p進數對於同餘信息有一種獨特的編碼方法,這在數論里作用很大。例如,困擾數學家長達三百多年的費馬最後定理,終於在1994年由安德魯·懷爾斯使用p進數理論證明,這是數學上的重大突破。懷爾斯因此獲得2005年度邵逸夫獎。
量子物理
p進數剛出現時,學者們最初認為這理論屬於純數學領域,毫無任何實用價值。但1968年,兩位純數學研究者A. Monna和F. Van Der Blij首先提出將p進數套用到物理學中。1972年,E. Beltrametti和G. Cassinelli探討了一種取值為p進數的量子邏輯狀態模型。進入二十世紀八十年代後,p進數在量子物理學中的套用愈為廣泛。首先湧現的是p進弦和p進超弦模型。量子物理學家在這些模型中使用與實數拓撲性質不同的p進數,以構建出不同的時空結構,描述在普朗克尺度下與大尺度完全不同的物理現象和行為。在普朗克尺度下,基於實數的模型無法很好的描繪出某些量子特性,而p進數域的某些性質,比如說無序性,和普朗克尺度下的物理特質相近。
p進數量子物理學中的套用也帶動了數學中對p進數的研究。例如p進弦論的研究促使數學家展開了對p進數上的分布理論、微分方程及偽微分方程(pseudodifferential equation)、機率論以及p進數上相應希爾伯特空間(裝備了額外結構的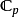 )中的運算元譜理論等多方面的研究。
)中的運算元譜理論等多方面的研究。
信息編碼
p進數的數列展開表示可以被用於信息的編碼。因此p進數可以被用來描述很多信息處理的過程,在認知科學、心理學和社會學研究中出現。
動力系統理論
算術動力系統是二十世紀九十年代提出的數學理論,整合了動力系統及數論。傳統的離散動力系統會探討疊代函式在複平面或是實數中的性質。算術動力系統則探討多項式或解析函式在整數、有理數、p進數及幾何點中的疊代特性。p進數動力系統在計算機科學領域中的直線式程式(straight-line programs)問題、數值分析與模擬中的偽隨機數問題、密碼學中的流加密問題上都有重要作用。在計算機科學和自動機理論中,p進遍歷理論可以幫助快速製造大拉丁方。後者在實驗設計、軟體測試和通信理論中都有良多套用。