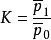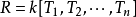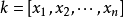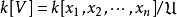交換代數

在抽象代數中，交換代數旨在探討交換環及其理想，以及交換環上的模。代數數論與代數幾何皆奠基於交換代數。交換環中最突出的例子包括多項式環、代數整數環與p進數環，以及它們的各種商環與局部化。

由於概形無非是交換環譜的黏合，交換代數遂成為研究概形局部性質的主要語言。

基本介紹

• 中文名：交換代數
• 外文名：commutative algebras
• 屬於：交換環的一門代數學科
• 套用學科：數學
• 相關術語：交換環
• 所屬領域：代數數論和代數幾何

定義

作為代數幾何的代數工具，還需要比交換環更進一步的代數結構，這就是「環上的代數」。A稱為環R上的代數（或簡稱為R代數），是指：①(A,+ ,·)為環，②（A，+）為R 模，③對於每個r∈R，α、b∈A，r(αb)=(rα)b=α(rb)。若A又是交換環，則稱A為R上的交換代數。R上的交換代數A稱為有限生成的，是指存在有限個元素 ，使得 。　設k為域， 為多項式環， 是R 的商域。著名的希爾伯特第14問題是對於k和E的每箇中間域l，l∩R作為k代數都是有限生成的。利用不變數理論，日本數學家中田於20世紀70年代舉出反例，否定了希爾伯特這個猜想,雖然這個猜想在n=1時是正確的。
設k是代數封閉域，kⁿ中代數簇V對應著 的根式理想U，則V的仿射坐標環 是k上有限生成的交換代數，並且沒有非零的冪零元素。反之，k上每個這種類型的交換代數均是k上某個代數簇的仿射坐標環，並且從代數簇V到代數簇W的多項式映射誘導出k[W]到k[V]的k代數同態。從而V和W同構(即存在互逆的兩個多項式映射)的充分必要條件是k[W]和k[V]作為k代數是同構的。於是，k上代數簇的同構分類相當於一種特殊類型的k上交換代數的同構分類。

歷史溯源

18世紀末到19世紀中期，C.F.高斯和E.E.庫默爾等人在研究關於有理整數性質和方程的有理整數解的時候，把這些初等數論問題放在二次域、分圓域以及它們的代數整數環中考慮，經過J.W.R.戴德金和D.希爾伯特等人的抽象化和系統化，形成了研究代數數域和它的代數整數環的一個新學科即代數數論。比數論稍晚些時候，幾何學也經歷了代數化過程，從19世紀末開始，由於希爾伯特等人的工作，特別是20世紀20～30年代德國女數學家(A.)E.諾特關於理想準素分解的理論和W.克魯爾建立的賦值論、局部環理論和維數理論，為古典幾何提供了全新的代數工具。從此，交換代數也成為一門獨立的學科。在20世紀50年代以後，交換代數得到很大發展，模論的研究、同調代數和各種上同調理論的建立，特別是法國數學家A.格羅騰迪克的概型理論，對於交換代數的發展起了巨大的推動作用。概型理論是算術幾何化的過程的理論，它將數論和射影代數幾何賦以新的高度統一的觀點。利用概型理論，P.德利涅於70年代初證明了A.韋伊關於有限域上射影代數簇ζ函式的一個著名猜想。現在，交換代數的運用已深入到微分與代數拓撲、多複變函數論、奇點理論、甚至偏微分方程等學科。

根和根式理想

以下的環均指含麼交換環。環R中全部素理想構成的集合，稱為R的(素)譜，記作Spec(R)。設U是環R的真理想，(即U≠R)，則R中至少存在一個包含U的素理想，所有包含U的素理想的交稱為U的根，記作 或 。事實上， 。顯然， 。若 ，則稱U為根式理想。特別當U=(0)（零理想）時， 就是R中全部冪零元構成的理想，稱為環R 的根。設k是代數封閉域，在代數幾何中，n維仿射空間k中的代數簇和多項式環 中的根式理想是反序(對於包含序)一一對應的，並且k中不可約代數簇和R的素理想也是反序一一對應的，這是代數幾何的基點。

擴展

分式環和

環R的子集S稱為乘法集，是指①1∈S；②α丶b∈S崊αb∈S，在集合R×S上定義關係～：(α,s)～(α′,s′)若存在t∈S使得t(αs′- α′s)=0。～是等價關係。以 表示元素（α,s）的等價類，S^-1R表示全部等價類組成的集合。對於加法 和乘法 ，S^-1R是含麼交換環，稱為R對於乘法集S的分式環。映射ƒ:R→S^-1R， 是環同態，其核為Kerƒ={α∈R|存在s∈S使得sα=0}。若S中非零元素均不是R的零因子，則ƒ為單射。從而R可看成S^-1R的子環。當R為整環而S=R-{0}時，S^-1R就是R 的商域。設M為R模而S為R的乘法集，可以類似地定義M對於S的分式模S^-1M，這是S^-1R模。　最重要的分式環是取S=R-β，其中β為R的素理想，這時S^-1R記為R_β，稱為R在β處的局部化。R_β是局部環（即只有惟一極大理想的環）。類似地對S=R-β可定義R模M在β處的局部化S^-1M，這是R_β模，並記為M_β。
S^-1:M→S^-1M是從R模範疇到S^-1R模範疇的正合函子，它有許多好的性質。它與模的許多運算都是可交換的，並且保持模和（當S^-1作用於環範疇時）環的許多性質，從而得到廣泛的套用，其中重要套用之一是所謂局部－整體原則。關於環（或者模）的某個性質P稱為局部性質，是指對於每個環R(或者R模M)，R（或者M_β）有性質P匔對於R的每個素理想β)，Rβ(或者Mβ)均有性質P。環和模有不少性質是局部性質。設P是局部性質。為了對某個環R(或者R模M)檢驗是否有性質P，只需對每個局部化R_β(或者M_β)來檢驗即可。由於R_β和Mβ比R和M結構簡單，因此由局部性質來掌握整體特性是研究環和模的重要手段，也是代數幾何和代數數論的重要研究工具。例如在代數幾何中採用局部化方法研究代數簇在一點附近的局部特性（如奇異性、相交重數等）。

諾特環

環R稱為諾特環，是指R的理想均是有限生成的。例如域和主理想整環都是諾特環。著名的希爾伯特基本定理是說，如果R為諾特環，則多項式環R【x₁,x₂,…,x_n】也是諾特環。特別當k是域時，k【x₁,x₂,…,x_n】是諾特環。
環R中的理想q稱為準素的，是指x丶y∈R，若xy∈q，必有x∈q或y∈q。諾特環的最重要性質是：每個理想均可表為有限個準素理想之交。由此推出，每個根式理想可以不計次序惟一地表成有限個彼此不包含的素理想之交。當k為代數封閉域時，由代數簇(不可約代數簇)和諾特環k【x₁,x₂,…,x_n】中根式理想(素理想)的反序對應即知，kⁿ中每個代數簇均可惟一地表成有限個彼此不包含的不可約代數簇之並，這就把kⁿ中代數幾何歸結為不可約代數簇的研究，或者說，歸結為諾特環 的素譜Spec(R)的研究。

戴德金整環

設R為環S的子環。S中元素s稱為在R上整的，是指存在首項係數是 1 的非零多項式 ƒ(x)∈R【x】，使得ƒ(s)=0。S中在R上整的全部元素是S的子環，稱為R在S中的整閉包。若這個整閉包等於R，則稱R在S中整閉。整環R稱為整閉的，是指R在其商域中整閉。
整環D稱為戴德金整環，是指：①D是整閉的，②D是諾特環，③D中非零素理想都是極大理想。每個主理想整環都是戴德金整環。任意代數數域K的代數整數環O_K(它是有理整數環Z 在K 中的整閉包)是戴德金整環。
戴德金整環D最值得注意的性質有兩個：①D中每個非零真理想均可不計次序惟一地表成有限個素理想之積，於是D的全體非零理想對於乘法是以全體非零素理想為基的自由交換么半群。它所擴張成的自由交換群稱為D的分式理想群I(D)，I(D)中元素稱為D的分式理想，它是兩個理想之商。戴德金整環O_K中每個理想如何分解成素理想之積，是代數數論的一個重要研究課題。②D中全體主分式理想(α)（0≠α∈F，F為D的商域）形成I(D)的一個子群P(D)。商群C(D)=I(D)/P(D)稱為D的理想類群。
關於戴德金整環D的一個重要結果是：D為主理想整環匔D為惟一因子分解整環匔C(D)為一元群。對於任意代數數域K，理想類群C(O_K)是有限交換群，它的階稱為K的理想類數。研究代數數域的理想類群和類數，是代數數論的一個重要課題。

維數理論

設 是環R中素理想鏈，n稱為這個素理想鏈的長度。R中所有素理想鏈的長度的最大值（可能是無限的）稱為R的（克魯爾）維數，記作dimR 。設R是諾特局部環，M是它的惟一極大理想，對於每個準素理想q，以δ(q)表示生成理想q所需元素的最少個數，而δ(R)表示所有δ(q)（q過R的所有準素理想）的最小值，則dimR=δ(R)。進而，若R的惟一極大理想M本身可以由δ(R)個元素生成，則稱R為正則諾特局部環。
環的維數理論有直觀的代數幾何背景。域k上不可約代數簇V的維數dimV在代數幾何中定義為V的有理函式域k(V)在k上的超越次數。另一方面，對於V上每個點P，k(V)中在P正則的函式形成環，這是諾特局部環，稱為V在點P的局部環，它的維數稱為V在點P的局部維數，它等於V的維數，並且P是V的非奇異點匔V在點P的局部環是正則諾特局部環。

完備化

設U是環R的理想，取{Uⁿ|n≥0}為R中零元素的基本鄰域系，則R由此成為拓撲環。R中這個拓撲稱為U-adic拓撲，並且，R是豪斯多夫拓撲空間 。類似地，設M為R模，取 為零元素的基本鄰域系，則M由此成為拓撲R 模，並且M對於這種U-adic拓撲是豪斯多夫空間 。若 R 為諾特環而M是有限生成R 模，則對於R的每個真理想U，條件 和 滿足，這時，U－adic豪斯多夫空間R 和M可以拓撲完備化成環惵 和惵模 ，理想U作為R 模的完備化 是環惵 的理想，惵 和 由R(和M)中 U-adic拓撲誘導出的拓撲就是 -adic拓撲，並且 =惵M。完備化函子R→惵和M→ 保持環和模的許多特性，而將R或M完備化成惵或 之後的好處，是可以採用極限和收斂等解析工具，從而，完備化也是代數幾何和代數數論以及許多其他學科的重要研究手段。