基本介紹
- 中文名:合成代數
- 外文名:composition algebra
- 領域:數學
- 定義:對偶空間的張量積所成的代數
- 別稱:分數代數、分裂代數
- 判定定理:赫爾維茨定理
代數簡介,對偶空間,代數張量積,合成代數,發展歷史,
代數簡介
數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。例如: 1/2 xy+1/4z-3x+2/3. 一個代數方程式 (參見EQUATION)是通過使多項式等於零來表示對變數所加的條件。如果只有一個變數,那么滿足這一方程式的將是一定數量的實數或複數——它的根。一個代數數是某一方程式的根。代數數的理論——伽羅瓦理論是數學中最令人滿意的分支之一。建立這個理論的伽羅瓦(Evariste Galois,1811-32)在21歲時死於決鬥中。他證明了不可能有解五次方程的代數公式。用他的方法也證明了用直尺和圓規不能解決某些著名的幾何問題(立方加倍,三等分一個角)。多於一個變數的代數方程理論屬於代數幾何學,抽象代數學處理廣義的數學結構,它們與算術運算有類似之處。參見,如: 布爾代數(BOOLEAN ALGEBRA);群 (GRO-UPS);矩陣(MATRICES);四元數(QUA-TERNIONS );向量(VECTORS)。這些結構以公理 (見公理法 AXIOMATICMETHOD) 為特徵。特別重要的是結合律和交換律。代數方法使問題的求解簡化為符號表達式的操作,已滲入數學的各分支。
設K為一交換體. 把K上的向量空間E叫做K上的代數,或叫K-代數,如果賦以從E×E到E中的雙線性映射.換言之,賦以集合E由如下三個給定的法則所定義的代數結構:
——記為加法的合成法則(x,y)↦x+y;
——記為乘法的第二個合成法則(x,y)↦xy;
——記為乘法的從K×E到E中的映射(α,x)↦αx,這是一個作用法則;
這三個法則滿足下列條件:
a) 賦以第一個和第三個法則,E則為K上的一個向量空間;
b) 對E的元素的任意三元組(x,y,z),有
x(y+z)=xy+xz(y+z)x=yx+zx;
c)對K的任一元素偶(α,β)及對E的任一元素偶(x,y),有(αx)(βy)=(αβ) (xy).
設A為一非空集合. 賦予從A到K中的全體映射之集ℱ(A,K)以如下三個法則:
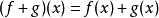
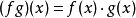
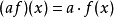
無論是在代數還是在分析中,代數結構都是最常見到的結構之一。十九世紀前半葉末,隨著哈密頓四元數理論的建立,非交換代數的研究已經開始。在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了。到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。
對偶空間
一種特殊的線性空間。即線性空間的線性函式空間。設V是域P上的線性空間,V的所有線性函式構成的域P上的線性空間,稱為V的對偶空間,記為V(即HomP(V,P)).當dim V=n,並且ε1,ε2,…,εn是V的基時,由等式εi(εj)=δij(i,j=1,2,…,n)所確定的n個線性函式ε1,ε2,…,εn是V的基,稱為基ε1,ε2,…,εn的對偶基。由上知,當dim V=n有限時,dim V=dim V=n;但當dim V無限時,二者不再相等,即它們的基元素不再是一一對應的。
代數張量積
代數張量積是構造新代數的一種重要方法。兩個R代數A,B作為R模的張量積A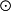 RB是由{x
RB是由{x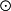 y|x∈A,y∈B}生成的R模,並具有泛性質(即對任一R代數P,作為模若Φ:A×B→P是R模雙線性平衡映射,則存在惟一的R模同態φ:A
y|x∈A,y∈B}生成的R模,並具有泛性質(即對任一R代數P,作為模若Φ:A×B→P是R模雙線性平衡映射,則存在惟一的R模同態φ:A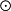 RB→P,使得對任意x∈A,y∈B恆有φ(x
RB→P,使得對任意x∈A,y∈B恆有φ(x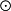 y)=Φ(x,y)),於是,在A
y)=Φ(x,y)),於是,在A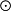 RB中存在一個乘法運算滿足:
RB中存在一個乘法運算滿足:
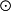
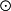
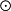
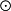
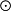
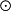
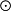
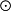
(x1,x2∈A;y1,y2∈B),
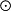
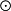
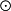
(A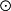 B)
B)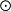 C
C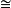 A
A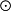 (B
(B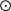 C),
C),
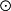
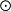
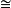
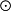
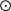
(A⊕B)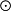 C
C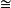 A
A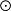 C⊕B
C⊕B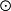 C,
C,
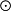
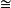
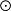
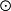
R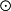 A
A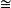 A
A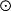 R
R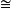 A.
A.
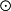
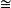
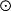
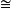
張量積對研究代數結構有重要意義。例如,域F上有限維單代數恆為F上n階全陣代數Fn與F上可除代數D的張量積。從而將有限維單代數的研究歸結為可除代數的研究。
合成代數
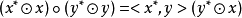
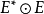
發展歷史
幾個早期作者注意到了平方和的組成。 Diophantus意識到涉及兩個平方的總和的性質,現在稱為“Brahmagupta-斐波納契”(Brahmagupta-Fibonacci)性質,這也被稱為複數的歐幾里得規範的屬性。 Leonhard Euler在1748年討論了四平方的身份,並引導W. R. Hamilton建立了四維數的四維代數。1848年,描述了一些給雙重複數的第一個光子。
約1818年,丹麥學者費迪南德·德根(Ferdinand Degen)展示了德根的八平方厘米特性,後來與八項代數元素的規範相聯繫:
歷史上,第一個非關聯代數,Cayley數...出現在二次形式的數論問題的上下文中,允許組合...這個數論問題可以轉化成一個關於某些代數系統,合成代數的問題。
在1919年,倫納德·迪克森(Leonard Dickson)通過對該日期的努力進行了調查,提出了對赫爾維茨問題的研究,並展示了將四元數加倍以獲得凱利數字的方法。他引入了一個新的虛構單位e,對於四元數q和Q寫出一個Cayley數q + Qe。用q'表示四元數共軛,兩個Cayley數的乘積為:
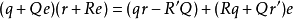
Cayley數的共軛是q'-Qe,二次形式是qq'+ QQ',通過將該數乘以其共軛而獲得。加倍方法已經被稱為Cayley-Dickson構造法。
在1923年,具有正定形式的真正代數的情況由赫爾維茨定理(合成代數)界定。
在1931年,Max Zorn在Dickson結構中的乘法規則中引入了一個伽馬(γ),以產生分裂八次。阿德里安·阿爾伯特(Adrian Albert)在1942年也使用了伽馬,當時他表明,迪克森加倍可以套用於具有平方函式的任何領域,以二次形式構建二元數組,四元數和八次代數。內森·雅各布森(Nathan Jacobson)在1958年描述了合成代數的自動化。
R和C域上的經典合成代數是單位代數。沒有乘法性質的合成代數由H.P. Petersson(Petersson代數)和Susumu Okubo(Okubo algebras)等。
